Le 22.12.2014 Les moyens de calculs depuis 40 ans >>

Table d'orientation du site>>

SCIENCES & TECHNIQUES
Date heure
Informations générales : Energie, Structures, Espace, Climat, réalisations, calculs, ...
CALCULS
Le 28.02.2015 Le modèle proie/prédateur de Volterra-Lokta >>
Le 09.04.2015 Les jeux de hasard >>
Le 23.07.2015 Bonne résolution >>
Le 25.03.2016 La loi de Moore : la fin ?
Le 13.05.2016 Différences Finies Modèle 1D >>
Le 14.10.2016 Quelques notes >>
Le 07.02.2017 Echange convectif en paroi >>
Le 25.02.2017 Das Rätsel >>
Le 12.10.2017 Les jeux de hasard : correctif >>
Le 15.03.2020 Pandémie >>
Le 10.04.2020 Epidémiologie >>
Le 06.01.2021 Modèle épidémiologique >>
Le 29.11.2021 Le QR code >>
Le 04.05.2022 Lumière de phare >>
Le 16.06.2022 Retour sur le QR code >>
Le 16.06.2022
Retour sur le QR code
J'ai abordé le sujet du QR code ici même le 29/11/2021 ...
Mais je restais sur ma faim.
En effet l'usage montre, au moins pour les petites taille de matrices, qu'il s'agit de quelque chose d'assez complexe dans la mise en oeuvre pour ... peu de chose.
Dans la plupart des cas la lecture de ce code renvoie simplement ... vers une adresse internet.
Je vais prendre un exemple précis : ma carte d'électeur !
Mais je restais sur ma faim.
En effet l'usage montre, au moins pour les petites taille de matrices, qu'il s'agit de quelque chose d'assez complexe dans la mise en oeuvre pour ... peu de chose.
Dans la plupart des cas la lecture de ce code renvoie simplement ... vers une adresse internet.
Je vais prendre un exemple précis : ma carte d'électeur !
Première étape : une photo de la carte avec son QR code (matrice 29x29, QR Code de version 3, 35 à 77 caractères) et une photo du résultat de la lecture de ce code :

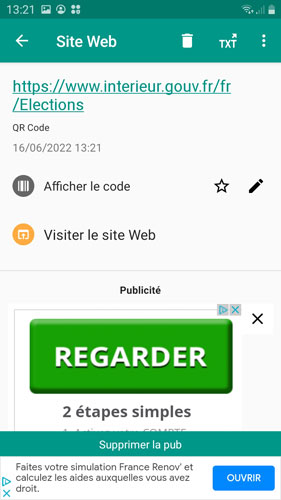
Le lien https://www.interieur.gouv.fr/fr/Elections (42 caractères) permet de se connecter au site officiel.
Je serais tenté de dire : tout cela pour ça !
De fait, ce QR code est identique sur toutes les cartes d'électeur (pas d'informations personnelles)
Je serais tenté de dire : tout cela pour ça !
De fait, ce QR code est identique sur toutes les cartes d'électeur (pas d'informations personnelles)
Cet exercice étant assez long, et faute de temps, je le réaliserai en plusieurs fois, cette rubrique sera donc complètée au fur et à mesure des semaines à venir ...
Alors comment s'y retrouver dans cette matrice 29x29, magma de pixels, à interpréter comme un ensemble d'informations binaires de 1 (croix) et de zéro (blancs) ?
Première opération, fastidieuse, j'ai transcrit la matrice sur une feuille de papier quadrillé pour la rendre plus lisible.
Il faut de bons yeux et de l'attention !!
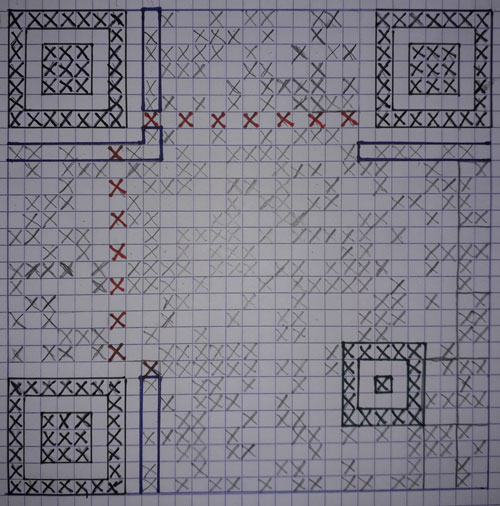
Ensuite identifier les principales zones :
Sur le coté droit, en partant du bas, j'ai juste commencé à identifier quelques octets (rectangles 2x4bits).
Première opération, fastidieuse, j'ai transcrit la matrice sur une feuille de papier quadrillé pour la rendre plus lisible.
Il faut de bons yeux et de l'attention !!
Ensuite identifier les principales zones :
- en noir (aux 2 angles supérieurs et à l'angle inférieur gauche) et vert (bas droit, sur la diagonale) les cibles d'alignement, zones interdites.
- en rouge les pointillés, zone interdite
- en bleu les deux zones de format, redondantes, en haut à gauche et celle coupée en deux morceaux à droite en haut et en bas à gauche. Cette zone fournit le niveau de correction et l'indice du masque.
- tout le reste (croix grises) concerne les données.
Sur le coté droit, en partant du bas, j'ai juste commencé à identifier quelques octets (rectangles 2x4bits).
La lecture des formats donne : 110100101110110 (redondance exacte)
Ici le masque binaire 101010000010010, défini dans le standard QR code, est utilisé pour décoder cet ensemble de bits avec un 'ou exclusif' (XOR : résultat VRAI si un et un seul des événements A et B est VRAI, au sens binaire 1 vrai, 0 faux)
Soit :
110100101110110
101010000010010
011110101100100 qui est donc la zone de format.
Ici le masque binaire 101010000010010, défini dans le standard QR code, est utilisé pour décoder cet ensemble de bits avec un 'ou exclusif' (XOR : résultat VRAI si un et un seul des événements A et B est VRAI, au sens binaire 1 vrai, 0 faux)
Soit :
110100101110110
101010000010010
011110101100100 qui est donc la zone de format.
- les deux premiers bits à gauche, 01, donnent le niveau de correction des erreurs, soit 1 (Niveau L, le plus bas)
- Les trois bits suivants, 111, donnent le numéro du masque, défini par une matrice A(i,j) de 0 et 1 de même dimension que le QR code, où les éléments sont calculés suivant une fonction des indices de ligne et colonne (évite de grande plages uniformes). Je renvoie à la référence [3]. Ici, traduit en décimal, c'est le masque n°7
- 0101100100, 10 bits du code de correction d'erreur calculés en utilisant le code BCH (!)
Il faut donc 'démasquer' les modules de données du QR code, c'est à dire décoder bit à bit avec un XOR en utilisant le masque n°7.
Ce masque a pour représentation mathématique :
(((i + j) mod 2) + ((i ∗ j) mod 3)) mod 2 == 0
Le motif est donné ci-contre, à répéter sur l'ensemble de la matrice, en partant du coin haut gauche.
Ce masque a pour représentation mathématique :
(((i + j) mod 2) + ((i ∗ j) mod 3)) mod 2 == 0
Le motif est donné ci-contre, à répéter sur l'ensemble de la matrice, en partant du coin haut gauche.

OU exclusif XOR :
| Données QR code | 1 | 1 | 0 | 0 |
| Masque | 1 | 0 | 1 | 0 |
| Résultat | 0 | 1 | 1 | 0 |
Pour ne pas me perdre dans l'opération (!), j'ai construit la matrice du masque, de même dimension que la matrice du QR code, en l'occurence 29x29.
Je superpose le masque sur le QR code et j'effectue l'opération logique qui va bien bien (tableau ci-dessus à droite), résultat dans une troisième matrice 29x29 qui peut être exploitée ...
Nota : j'aurais pu passer par une solution numérique en utilisant 2 matrices carrées de même dimension : A(i,j) remplie avec le QR code, B(i;j) remplie avec le masque puis réaliser terme à terme numériquement l'opération logique XOR mais je crois que cela était presque aussi bestial ....!
Je superpose le masque sur le QR code et j'effectue l'opération logique qui va bien bien (tableau ci-dessus à droite), résultat dans une troisième matrice 29x29 qui peut être exploitée ...
Nota : j'aurais pu passer par une solution numérique en utilisant 2 matrices carrées de même dimension : A(i,j) remplie avec le QR code, B(i;j) remplie avec le masque puis réaliser terme à terme numériquement l'opération logique XOR mais je crois que cela était presque aussi bestial ....!
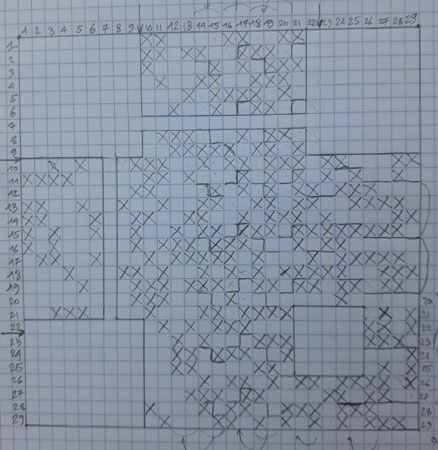
Le QR code démasqué
(les octets de données sont pointés)
(les octets de données sont pointés)
La matrice du masque

Enfin, que se cache-t-il dans ce QR code ?
Déjà, quelles données ?
Le mode est défini par les 4 premiers bits (en bas à droite), il fallait le savoir ....!!!
C'est la nature des données (numériques, alphanumériques, simple Byte sur 8 bits, ...)
La combinaison (mode, version du QR code) donne le nombre de bits du codage des données.
De même, l'octet suivant donne le nombre de caractères du message.
J'avoue que ces informations ne sont pas si faciles à trouver, j'ai dû piocher aussi dans toutes ces références [4,5,6,7,8,9] et d'autres encore ....
Déjà, quelles données ?
Le mode est défini par les 4 premiers bits (en bas à droite), il fallait le savoir ....!!!
C'est la nature des données (numériques, alphanumériques, simple Byte sur 8 bits, ...)
La combinaison (mode, version du QR code) donne le nombre de bits du codage des données.
De même, l'octet suivant donne le nombre de caractères du message.
J'avoue que ces informations ne sont pas si faciles à trouver, j'ai dû piocher aussi dans toutes ces références [4,5,6,7,8,9] et d'autres encore ....
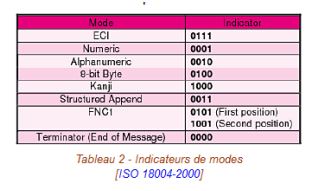
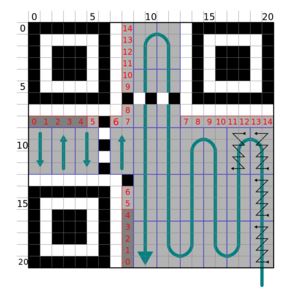
Remarque : attention à l'ordre de lecture des bits !
Illustration sur une matrice 21x21, applicable à toute version :
Illustration sur une matrice 21x21, applicable à toute version :
- démarrage en bas à droite,
- de droite à gauche,
- de bas en haut.
Ordonnancement des octets pour notre QR code 29x29.
Mais en réalité il existe un décalage dès le début avec la définition du mode sur 4 bits.
Cela ne change pas l'ordre de lecture des bits.
Mais en réalité il existe un décalage dès le début avec la définition du mode sur 4 bits.
Cela ne change pas l'ordre de lecture des bits.
Revenons à nos moutons, notre matrice démasquée. Enfin, nous allons savoir !
Il faut lire bit à bit, octet après octet, transposition binaire/décimal, décodage caractère ASCII/ ISO-8859-1.
4 premier bits Mode : 0100 > données sur 8 bits
1er Octet Nombre de caractères : 00101010 > (32+8+2)=42 (chouette, c'est exactement la longueur du lien trouvé sur la carte, voir le début de la chronique)
et ainsi de suite ....
Pour ne pas alourdir la page le décodage des 42 octets, représentation du texte https://www.interieur.gouv.fr/fr/Elections, est présenté dans ce fichier.
CQFD !!
Il faut lire bit à bit, octet après octet, transposition binaire/décimal, décodage caractère ASCII/ ISO-8859-1.
4 premier bits Mode : 0100 > données sur 8 bits
1er Octet Nombre de caractères : 00101010 > (32+8+2)=42 (chouette, c'est exactement la longueur du lien trouvé sur la carte, voir le début de la chronique)
et ainsi de suite ....
Pour ne pas alourdir la page le décodage des 42 octets, représentation du texte https://www.interieur.gouv.fr/fr/Elections, est présenté dans ce fichier.
CQFD !!
On notera qu'il n'y a pas d'erreur dans le décodage (= le QR code n'est pas dégradé sur ma carte).
Reste tout un ensemble de bits, précisément 27 octets (n° 43 à 69) plus trois bits seuls, qui concerne justement la correction d'éventuelles erreurs qui seraient liées à une dégradation du QR code.
Là c'est un peu plus compliqué.
Reste tout un ensemble de bits, précisément 27 octets (n° 43 à 69) plus trois bits seuls, qui concerne justement la correction d'éventuelles erreurs qui seraient liées à une dégradation du QR code.
Là c'est un peu plus compliqué.
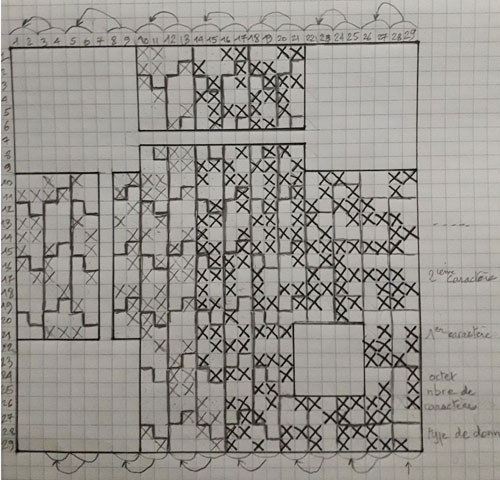
Pour plus de clarté j'ai repris la matrice (j'ai corrigé une erreur) de mon QR code démasqué vue plus haut en accentuant au feutre uniquement les bits des 42 caractères (octets) de données.
Le décodage des 27 octets suivants et correspondant à la correction d'erreur est présenté ici.
Mais pour l'instant je ne sais quoi en faire : il faut que je me plonge dans la méthode Reed Solomon...
Et cela n'a pas l'air simple !
Le décodage des 27 octets suivants et correspondant à la correction d'erreur est présenté ici.
Mais pour l'instant je ne sais quoi en faire : il faut que je me plonge dans la méthode Reed Solomon...
Et cela n'a pas l'air simple !
L'utilisation du QR code pour cet exemple peut paraitre disproportionnée. C'est vrai.
Mais toutes ces opérations sont aujourd'hui complètement maitrisées, programmées, archi-codifiées pour toutes versions de QR code, de la plus simple à la plus complexe, aussi bien dans le sens écriture que lecture.
Et puis restons curieux !
Mais toutes ces opérations sont aujourd'hui complètement maitrisées, programmées, archi-codifiées pour toutes versions de QR code, de la plus simple à la plus complexe, aussi bien dans le sens écriture que lecture.
Et puis restons curieux !
↑ Haut de page ↑
Le 04.05.2022
Lumière de Phare
Je l'avais cotoyé pendant 2 ans : le phare de l'ile Vierge à la pointe du Finistère nord
J'en ai déjà présenté la structure mais difficile d’imaginer une portée de l'ordre de 50km avec une lampe halogène de 250 W !
Le phare a été électrifié à la fin des années 1950 et l’optique double d’origine remplacée par une nouvelle optique, à quatre panneaux au 1/4 dans un caisson moulé, fixée sur l’ancienne base tournante reposant sur la cuve à mercure de grande taille ‘Barbier et Bénard’ d’origine !
Le foyer est à ~75m de hauteur
La lanterne a un diamètre de 4 m, à 3 niveaux de vitrage cylindrique.
Eclats réguliers blancs toutes les 5 sec, focale de 0,50 m.
Je m'intéresse ici aux caractéristiques optiques et à la manière dont la portée peut être explicitée.
J'en ai déjà présenté la structure mais difficile d’imaginer une portée de l'ordre de 50km avec une lampe halogène de 250 W !
Le phare a été électrifié à la fin des années 1950 et l’optique double d’origine remplacée par une nouvelle optique, à quatre panneaux au 1/4 dans un caisson moulé, fixée sur l’ancienne base tournante reposant sur la cuve à mercure de grande taille ‘Barbier et Bénard’ d’origine !
Le foyer est à ~75m de hauteur
La lanterne a un diamètre de 4 m, à 3 niveaux de vitrage cylindrique.
Eclats réguliers blancs toutes les 5 sec, focale de 0,50 m.
Je m'intéresse ici aux caractéristiques optiques et à la manière dont la portée peut être explicitée.

En lisant différents papiers sur ce sujet je me suis demandé comment calculer cette portée qui, par ailleurs, pouvait simplement résulter de l’observation.
Dans tout ce qui suit
J’ai tiré sur le fil …
La notion de portée peut être interprétée de différentes façons, en prenant en compte tous les paramètres, des + simples aux + complexes.
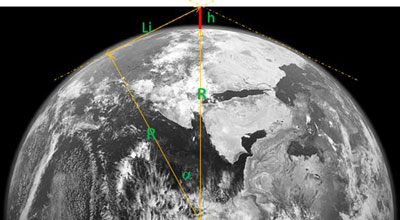
La première démarche basique conduit à calculer son ‘horizon ‘, soit la limite de visibilité à l’horizon, notée Li (les proportions des schémas sont exagérés pour la compréhension):
Dans tout ce qui suit
- R= 6371 km est le rayon terrestre
- h : la hauteur du foyer du phare par rapport au niveau de la mer, en l’occurrence ici h # 75m.
J’ai tiré sur le fil …
La notion de portée peut être interprétée de différentes façons, en prenant en compte tous les paramètres, des + simples aux + complexes.
La première démarche basique conduit à calculer son ‘horizon ‘, soit la limite de visibilité à l’horizon, notée Li (les proportions des schémas sont exagérés pour la compréhension):
(R+h)2 = R2 + Li2 (Pythagore !)
Li2 = (R+h)2 - R2 = (2Rh) car h2<<2Rh (rapport de ~ 10-6)
Li= (2Rh)1/2 # 112,9 (2Rh)1/2
Li # 3,57.(h)1/2 avec h en m, Li en km [1]
Li=30,9 km
Ou aussi (pourquoi faire simple quand on peut faire compliqué) :
tg α = Li/R
R/(R+h)=cos α soit α = Acos [R/(R+h)]
Li= R . tg α= R . tg(Acos [R/(R+h)])
Li= R . tg(Acos [R/(R+h)]) [2]
Soit Li=30,9 km (heureusement, même résultat entre [1] et [2] à 10-4 près)
Li2 = (R+h)2 - R2 = (2Rh) car h2<<2Rh (rapport de ~ 10-6)
Li= (2Rh)1/2 # 112,9 (2Rh)1/2
Li # 3,57.(h)1/2 avec h en m, Li en km [1]
Li=30,9 km
Ou aussi (pourquoi faire simple quand on peut faire compliqué) :
tg α = Li/R
R/(R+h)=cos α soit α = Acos [R/(R+h)]
Li= R . tg α= R . tg(Acos [R/(R+h)])
Li= R . tg(Acos [R/(R+h)]) [2]
Soit Li=30,9 km (heureusement, même résultat entre [1] et [2] à 10-4 près)
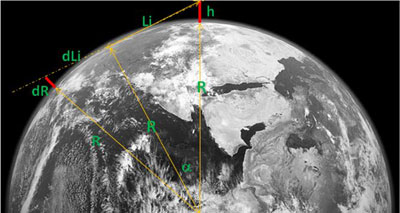
Remarque : en théorie cette portée se trouve augmentée de dLi pour tout objet de hauteur dR situé au-delà du point de limite de visibilité.
dLi2 + R2 = (R+dR)2
Comme (R+dR)2 ~ R2 + 2RdR (dR2 petit devant R2 et devant 2RdR) :
dLi2 = 2RdR
dLi = (2RdR)1/2
La portée totale vaut :
Li +dLi = (2Rh)1/2 + (2RdR)1/2
(Li +dLi) = (2R)1/2 [(h)1/2 + (dR)1/2]
Dans notre exemple précédent la portée de 30,9km passe à 38,9km (+ 8km) pour un objet dR de 5m de hauteur …
dLi2 + R2 = (R+dR)2
Comme (R+dR)2 ~ R2 + 2RdR (dR2 petit devant R2 et devant 2RdR) :
dLi2 = 2RdR
dLi = (2RdR)1/2
La portée totale vaut :
Li +dLi = (2Rh)1/2 + (2RdR)1/2
(Li +dLi) = (2R)1/2 [(h)1/2 + (dR)1/2]
Dans notre exemple précédent la portée de 30,9km passe à 38,9km (+ 8km) pour un objet dR de 5m de hauteur …
L'objet dR' de même hauteur de 5m peut être vu de plus loin encore si on tient compte de la réfraction de l'atmosphère (voir fig 2 du lien et l'approche théorique).
Mais l'article ne répond pas complètement à la question. Quid de la longueur de l'arc dLi' ?
Mais l'article ne répond pas complètement à la question. Quid de la longueur de l'arc dLi' ?
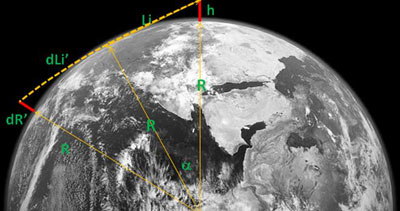
Par hypothèse, l'auteur considère que la courbure de cet arc (C) et celle de la terre (1/R) sont liées par la relation k=C/1/R=C.R
k est pris égal à 0,16, sachant que cette valeur est très dépendante des conditiopns météorologiques locales.
Notons que cela revient à considérer que la courbure du rayon lumineux est constante, ce qui n'est pas exactement le cas.
Approximation : l'arc de terre et l'arc lumineux sont assimilés à 2 arcs de paraboles respectivement de la forme y1=x2/2R et y2=k.x2/2R.
En effef l'équation générale du cercle de la terre projetée est :
x2 + (y-R)2 = R2
L'origine du repère est tangent à la terre (voir schéma)
En négligeant le terme en y2 (arc de courbe proche de l'origine) : y=x2/2R
k est pris égal à 0,16, sachant que cette valeur est très dépendante des conditiopns météorologiques locales.
Notons que cela revient à considérer que la courbure du rayon lumineux est constante, ce qui n'est pas exactement le cas.
Approximation : l'arc de terre et l'arc lumineux sont assimilés à 2 arcs de paraboles respectivement de la forme y1=x2/2R et y2=k.x2/2R.
En effef l'équation générale du cercle de la terre projetée est :
x2 + (y-R)2 = R2
L'origine du repère est tangent à la terre (voir schéma)
En négligeant le terme en y2 (arc de courbe proche de l'origine) : y=x2/2R
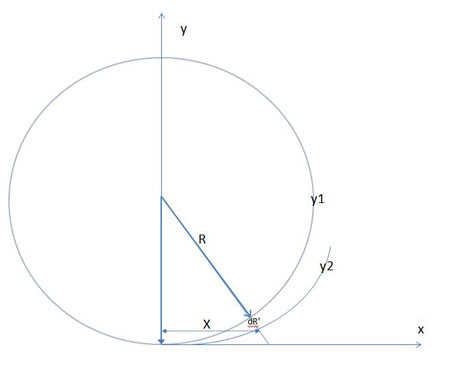
Le principe du calcul de la longueur L d'un arc de parabole ax2 entre deux bornes x1 et x2 est donné ici.(rare opportunité de l'utilisation de l'intégration par parties !)
Dans notre problème, x1=0.
La borne x2=X peut être calculée:par la relation
X2+(R-kX2/2R)2 = (R+dR')2. où y vaut k.x2/2R
Soit X2.(1-k) # 2.R.dR' (kX4/4R2 et dR'2 négligeables)
ou X = [2.R.dR'/(1-k)]1/2
Soit ici X = [2.6371.0,005/(1-0,16)]1/2 = 8,70891716 km
L'arc lumineux à l'abcisse X doit être un peu plus long que X.
Pour la parabole générique ax2+bx+c, L est donnée par la relation :
L = 1/(2a).[F(z2) - F(z1)] avec
z1=2ax1+b
z2=2ax2+b
F(z)=1/2.[z.(1+z2)1/2+Log[z+(1+z2)1/2]
Ici b=0, a=k/2R, 1/(2a)=R/k
x1=0, x2=X
>>> z1=0 et z2=k.X/R=2,18695252 10-4
>>> F(z1)=0 et F(z2)=1/2.(2,18695258+2,18695251).10-4#2,1869.10-4
>>> L=dLi' # X car, à l'échelle et avec les approximations, le rayon lumineux est assimilable à sa projection.
La portée totale depuis notre phare jusqu'à l'objet de 5m est donc de (30,9 + 8,7)=39,6 km (+700m par rapport au cas précédent !!)
Dans notre problème, x1=0.
La borne x2=X peut être calculée:par la relation
X2+(R-kX2/2R)2 = (R+dR')2. où y vaut k.x2/2R
Soit X2.(1-k) # 2.R.dR' (kX4/4R2 et dR'2 négligeables)
ou X = [2.R.dR'/(1-k)]1/2
Soit ici X = [2.6371.0,005/(1-0,16)]1/2 = 8,70891716 km
L'arc lumineux à l'abcisse X doit être un peu plus long que X.
Pour la parabole générique ax2+bx+c, L est donnée par la relation :
L = 1/(2a).[F(z2) - F(z1)] avec
z1=2ax1+b
z2=2ax2+b
F(z)=1/2.[z.(1+z2)1/2+Log[z+(1+z2)1/2]
Ici b=0, a=k/2R, 1/(2a)=R/k
x1=0, x2=X
>>> z1=0 et z2=k.X/R=2,18695252 10-4
>>> F(z1)=0 et F(z2)=1/2.(2,18695258+2,18695251).10-4#2,1869.10-4
>>> L=dLi' # X car, à l'échelle et avec les approximations, le rayon lumineux est assimilable à sa projection.
La portée totale depuis notre phare jusqu'à l'objet de 5m est donc de (30,9 + 8,7)=39,6 km (+700m par rapport au cas précédent !!)
Autre question que je m'étais posée : même à proximité du phare, le faisceau lumineux, théoriquement cohérent et parallèle, est visible .....
Tout ce qui suit s'inspire du site qui présente les inventions de Fresnel dans le domaine de l'optique des phares et balises.
Pour optimiser la masse de la lentille Fresnel a imaginé une structure à échelons qui par ailleurs conserve les propriétés optiques.
Tout ce qui suit s'inspire du site qui présente les inventions de Fresnel dans le domaine de l'optique des phares et balises.
Pour optimiser la masse de la lentille Fresnel a imaginé une structure à échelons qui par ailleurs conserve les propriétés optiques.
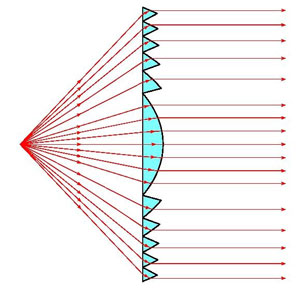
Pourquoi ce faisceau est-il en réalité très vite divergent ?
On peut en attribuer une part à la qualité de l'atmosphère, que ce soit poussières ou humidité qui agissent comme autant d'éléments diffractants.
On peut en attribuer une part à la qualité de l'atmosphère, que ce soit poussières ou humidité qui agissent comme autant d'éléments diffractants.

Le foyer de la lentille est un point théorique à partir duquel émet la source. Dans la réalité cette source, constituée d'une lampe halogène de 250W, n'est pas ponctuelle comme le montre la photo ci-contre.
Je ne connais pas toutes les dimensions du système sauf la focale, qui est de 50cm.
En proportion du diamètre des lentilles la lampe a une hauteur, à vue d'oeil, de peut-être 5% de ce diamètre.
Je ne connais pas toutes les dimensions du système sauf la focale, qui est de 50cm.
En proportion du diamètre des lentilles la lampe a une hauteur, à vue d'oeil, de peut-être 5% de ce diamètre.
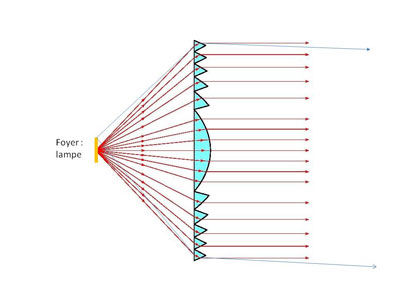
Faute de cotes exactes je me suis dispensé d'un calcul (sin i = n sin r !) mais on voit bien à partir d'un point haut de la lampe le cheminement des rayons lumineux (lignes bleues) qui ne sont plus tout à fait parallèles en sortie de lentille ...
Pour un observateur, cette divergence peut se ressentir rapidement (à calculer)
CQFD.
Pour un observateur, cette divergence peut se ressentir rapidement (à calculer)
CQFD.
↑ Haut de page ↑
Le 26.11.2021
Le QR code
L'existence du QR code s'est pleinement révélée ... avec la pandémie !
Aujourd'hui son utilisation a explosé dans tous les domaines de la vie courante.
Ce codage d'informations, qui n'est que l'extension à 2 dimensions du code barre, existe depuis le milieu des années 1990. L'entreprise japonaise qui l'a développé a eu l'intelligence de ne pas en verrouiller l'utilisation, qui est libre et gratuite (simplement respecter la norme)
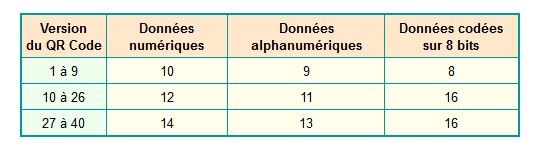
Avantage, il permet de stocker beaucoup plus d'informations, jusqu'à 7089 caractères numériques, 4296 caractères alphanumériques dans la version V40 (matrice 177x177) !
Comme chacun a pu le constater, ce QR code [1,2, ...] est donc contitué d'une matrice carrée (il existe une variante rectangulaire) d'un ensemble de petits carrés noirs ou blancs.
Analysons cette matrice :
Aujourd'hui son utilisation a explosé dans tous les domaines de la vie courante.
Ce codage d'informations, qui n'est que l'extension à 2 dimensions du code barre, existe depuis le milieu des années 1990. L'entreprise japonaise qui l'a développé a eu l'intelligence de ne pas en verrouiller l'utilisation, qui est libre et gratuite (simplement respecter la norme)
Avantage, il permet de stocker beaucoup plus d'informations, jusqu'à 7089 caractères numériques, 4296 caractères alphanumériques dans la version V40 (matrice 177x177) !
Comme chacun a pu le constater, ce QR code [1,2, ...] est donc contitué d'une matrice carrée (il existe une variante rectangulaire) d'un ensemble de petits carrés noirs ou blancs.
Analysons cette matrice :
- Trois sous-carrés particuliers (chaque angle de la matrice sauf angle bas droit) servent à indiquer la position du code QR et la façon il faut lire les données qui s’y trouvent (position detection patterns)
- Les 2 bandes (horizontale et verticale) comme des pointillés définisssent le positionnement des lignes et des colonnes (timing pattern)
- D’autres motifs sont disséminés, en plus des données à encoder elles-mêmes.
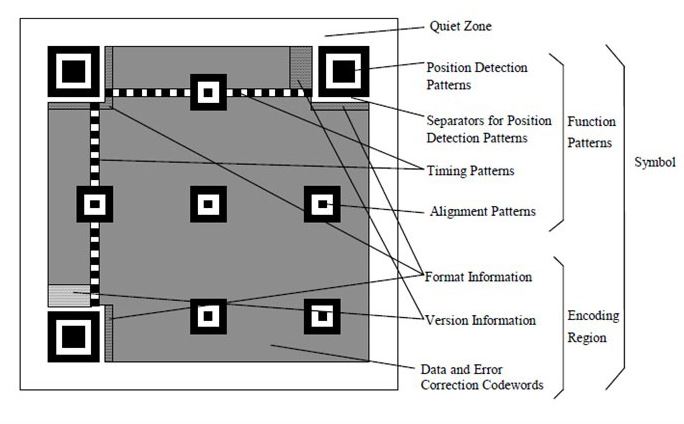
Credit Numerama.com
La redondance, ou correction d'erreur, est utilisée afin de reconstituer l'intégralité de l'information codée dans le QR code, même si celui-ci subit une altération (déchirure, tâche, froissure, ...). Ainsi l'information est répétée de façon à pouvoir à être retranscrite.
Le correcteur type utilisé ici est le code de Reed-Solomon (amélioration de la qualité de la communication et diminution du rapport signal/bruit). Je laisse le lecteur intéressé (et spécialiste !) se plonger dans les très nombreuses (et complexes) références sur Internet [1, 2, ...]
La redondance est visible sur un QR code dans sa structure. En effet plus un QR code a un taux de redondance élevé plus sa structure sera complexe mais moins il sera sensible aux dégradations.
4 taux de redondance (H, Q, M, L) ou perte d'information tolérée (en %) : 30, 25, 15, 7
La création d'un QR code se fait en plusieurs étapes :
Le correcteur type utilisé ici est le code de Reed-Solomon (amélioration de la qualité de la communication et diminution du rapport signal/bruit). Je laisse le lecteur intéressé (et spécialiste !) se plonger dans les très nombreuses (et complexes) références sur Internet [1, 2, ...]
La redondance est visible sur un QR code dans sa structure. En effet plus un QR code a un taux de redondance élevé plus sa structure sera complexe mais moins il sera sensible aux dégradations.
4 taux de redondance (H, Q, M, L) ou perte d'information tolérée (en %) : 30, 25, 15, 7
La création d'un QR code se fait en plusieurs étapes :
- Créer une chaîne de bits de données à partir du message que l'on veut encoder. ...
- Générer le code correcteur d'erreur (redondance)... Un exemple de création de ce code d'erreur est donné dans cet article.
- Choisir la meilleure forme de masque afin d'optimiser la lecture du QR code.
Je ne vais pas explorer ici en détail toutes les phases de l'écriture d'un QR code depuis sa création, l'encodage des données, la redondance, sa lecture, etc ... La référence citée précédemment, sur laquelle je m'appuie dans l'exemple ci-dessous, répond à ces questions.
En fait ce qui m'intéressait était de voir comment l'information (une donnée, quelle qu'elle soit), objet principal du système, est codée.
Prenons l'exemple d'un texte simple : BONJOUR
1-Choisir la version du QR code. Le message étant ici très simple (7 caractères), on choisit la plus petite version du QR code : matrice 21x21 (25c max).
Il existe un grand nombre de taille de matrice : 25x25 (47c max), 29x29 (77c max), 33x33 (114c max), 57x57 (395C max), 177x177 (4296c max), etc ... à choisir en fonction de la taille de l'information à coder.
2-Définir le type de donnée : alphanumérique Code : 0010
3-Longueur du message, fonction [type QR code, type d'information] : 7c sur 9bits, soit 000000111 en binaire.
>>>>> L'expression à ce stade est donc : 0010 000000111
4-Encodage des données : découpage en paires de caractères /BO/NJ/OU/R codées sur 11 bits, sauf le dernier caractère, tout seul ici, codé sur 6 bits.
Ensuite, pour minimiser le nombre de bits, on utilise un code 'ASCII simplifié' suivant ce tableau :
En fait ce qui m'intéressait était de voir comment l'information (une donnée, quelle qu'elle soit), objet principal du système, est codée.
Prenons l'exemple d'un texte simple : BONJOUR
1-Choisir la version du QR code. Le message étant ici très simple (7 caractères), on choisit la plus petite version du QR code : matrice 21x21 (25c max).
Il existe un grand nombre de taille de matrice : 25x25 (47c max), 29x29 (77c max), 33x33 (114c max), 57x57 (395C max), 177x177 (4296c max), etc ... à choisir en fonction de la taille de l'information à coder.
2-Définir le type de donnée : alphanumérique Code : 0010
3-Longueur du message, fonction [type QR code, type d'information] : 7c sur 9bits, soit 000000111 en binaire.
>>>>> L'expression à ce stade est donc : 0010 000000111
4-Encodage des données : découpage en paires de caractères /BO/NJ/OU/R codées sur 11 bits, sauf le dernier caractère, tout seul ici, codé sur 6 bits.
Ensuite, pour minimiser le nombre de bits, on utilise un code 'ASCII simplifié' suivant ce tableau :
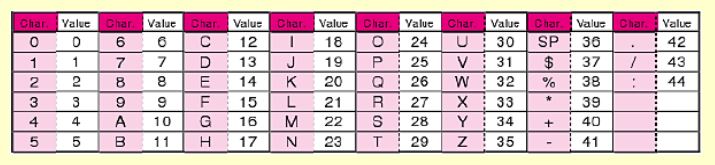
5-Pour chaque paire :
NJ : (11x45)+19 = 514, soit 01000000010
OU : (24x45)+30 = 1110, soit 10001010110
R : 27, soit 011011
Au final pour notre expression, nous avons le codage suivant :
0010 000000111 00110000000 01000000010 10001010110 011011
6-Rajouter le marqueur de fin 0000 :
0010 000000111 00110000000 01000000010 10001010110 011011 0000
7-Découpage de la chaine par octet (8 bits) :
00100000 00111001 10000000 01000000 01010001 01011001 10110000 (ici pile 7 octets)
8-Le QR-Code que nous désirons fabriquer est de version 1, avec 104 bits pour les données (niveau de correction Q, voir référence), soit 13 octets. Or notre expression binaire ne fait que 7 octets, il nous faut ajouter encore 6 octets qui seront 2 octets spécifiques, codes ASCII des nombres 236 et 17, répétés 3 fois soit 11101100 00010001 11101100 00010001 11101100 00010001
Notre expression vaut maintenant 00100000 00111001 10000000 01000000 01010001 01011001 10110000 11101100 00010001 11101100 00010001 11101100 00010001 (13 octets)
9-correction d'erreur (fondée sur le code de Reed-Solomon)
Ce calcul est assez complexe.
Un octet est caractérisé par un nombre N constitué de la concaténation de 2 nombres, N1 la somme des éléments de l'octet, N2 la
somme pondérée des éléments de l'octet, chacun étant multiplié par son rang ... Ouf
10- création de la matrice QR code
Après les informations obligatoires (spécifiques à chaque version de QR code) de positionnement, de séparateurs, du timing pattern et des motifs d'alignement, nous pouvons enfin placer nos octets de données !
Attention : elles doivent respecter un ordre qui dépend de la version du QR code
- prendre la valeur du code de la première lettre,
- Multiplier cette valeur par 45,
- Rajouter ensuite au résultat la valeur du code de la deuxième lettre.
- La valeur obtenue est par la suite transformée en une binaire sur 11 bits (6 bits)
NJ : (11x45)+19 = 514, soit 01000000010
OU : (24x45)+30 = 1110, soit 10001010110
R : 27, soit 011011
Au final pour notre expression, nous avons le codage suivant :
0010 000000111 00110000000 01000000010 10001010110 011011
6-Rajouter le marqueur de fin 0000 :
0010 000000111 00110000000 01000000010 10001010110 011011 0000
7-Découpage de la chaine par octet (8 bits) :
00100000 00111001 10000000 01000000 01010001 01011001 10110000 (ici pile 7 octets)
8-Le QR-Code que nous désirons fabriquer est de version 1, avec 104 bits pour les données (niveau de correction Q, voir référence), soit 13 octets. Or notre expression binaire ne fait que 7 octets, il nous faut ajouter encore 6 octets qui seront 2 octets spécifiques, codes ASCII des nombres 236 et 17, répétés 3 fois soit 11101100 00010001 11101100 00010001 11101100 00010001
Notre expression vaut maintenant 00100000 00111001 10000000 01000000 01010001 01011001 10110000 11101100 00010001 11101100 00010001 11101100 00010001 (13 octets)
9-correction d'erreur (fondée sur le code de Reed-Solomon)
Ce calcul est assez complexe.
Un octet est caractérisé par un nombre N constitué de la concaténation de 2 nombres, N1 la somme des éléments de l'octet, N2 la
somme pondérée des éléments de l'octet, chacun étant multiplié par son rang ... Ouf
Exemple sur notre deuxième octet 00111001
N1=[0+0+1+1+1+0+0+1]=4
N2=[0x1+0x2+1x3+1x4+1x5+0x6+0x7+1x8]=20
soit N=420La correction d'erreur correspondant à notre 2ième octet contiendra le nombre 420 (à transformer en binaire). Ainsi de suite pour tous les octets.
10- création de la matrice QR code
Après les informations obligatoires (spécifiques à chaque version de QR code) de positionnement, de séparateurs, du timing pattern et des motifs d'alignement, nous pouvons enfin placer nos octets de données !
Attention : elles doivent respecter un ordre qui dépend de la version du QR code
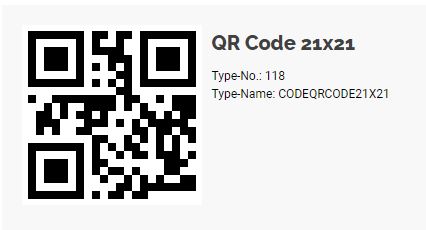
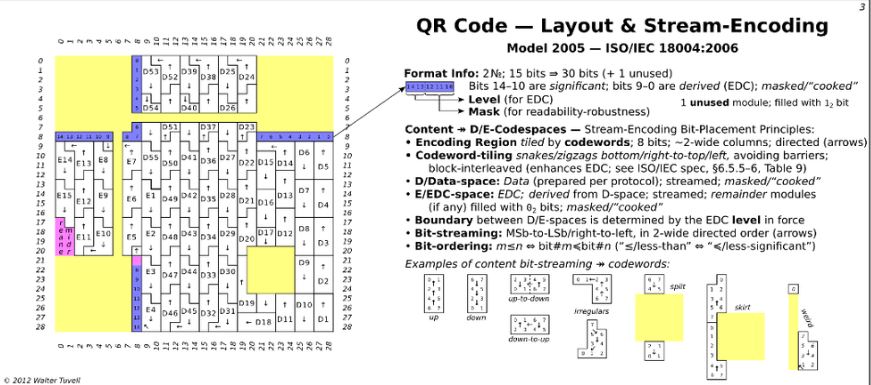
Exemple de QR code 21x21
Je n'ai pas trouvé le placement des octets pour une trame 21x21 (quoique cette référence en donne quelques éléments aux pages 20 et 30). L'exemple à droite s'applique à une trame 25x25.
On peut y repérer les octets d1 à d28 réservés aux données et les octets e1 à e16 réservés au code correcteur, soit au total 44 octets
On peut y repérer les octets d1 à d28 réservés aux données et les octets e1 à e16 réservés au code correcteur, soit au total 44 octets
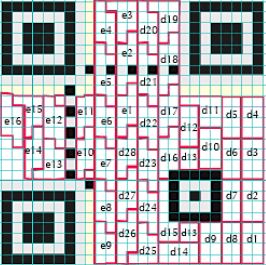
11-création d'un masque
Il évite de se retrouver avec des zones trop grandes de carrés foncés ou clairs les uns à côtés des autres
Il ne s’applique qu’aux octets de données et de correction d’erreurs, il modifie l"image du QR code.
8 types différents.
Il évite de se retrouver avec des zones trop grandes de carrés foncés ou clairs les uns à côtés des autres
Il ne s’applique qu’aux octets de données et de correction d’erreurs, il modifie l"image du QR code.
8 types différents.
Tout cela peut paraitre bien compliqué ... pour coder seulement le mot BONJOUR !
Et il faut ensuite le décoder !
Restons calme : aujoud'hui toutes ces informations sont générées automatiquement par logiciel. Et relues de même avec des lecteurs scanners adaptés !
Pour information il me semble que le QR code de mon certificat COVID est généré dans une matrice 80x80.
Et il faut ensuite le décoder !
Restons calme : aujoud'hui toutes ces informations sont générées automatiquement par logiciel. Et relues de même avec des lecteurs scanners adaptés !
Pour information il me semble que le QR code de mon certificat COVID est généré dans une matrice 80x80.
↑ Haut de page ↑
Le 06.01.2021
Modèle épidémiologique
J'en avais parlé il y a quelques mois dans la rubrique du 17/05/2020 ...
Je me suis intérressé à l'une des méthodes de modélisation d'une épidémie. Je dis une car il en existe de nombreuses, plus ou moins complexes.
Il s'agit ici du modèle simple, dit SEIR : la description complète (définition, paramètres) en est donnée dans ce lien qui m'a inspiré.
C'est un modèle à compartiments, régit par quatre équations différentielles du 1er ordre.
Je me suis intérressé à l'une des méthodes de modélisation d'une épidémie. Je dis une car il en existe de nombreuses, plus ou moins complexes.
Il s'agit ici du modèle simple, dit SEIR : la description complète (définition, paramètres) en est donnée dans ce lien qui m'a inspiré.
C'est un modèle à compartiments, régit par quatre équations différentielles du 1er ordre.
Ces équations décrivent le comportement de 4 populations liées en elles :
S : personnes saines (susceptible)
E : personnes exposées non infectueuses (exposed), qui ne sont donc pas contagieuses
I : personnes infectées (infected)
R : personnes retirées (removed), guéries
avec la relation S + E + I + R = 1 (la population totale considérée, qui évolue au cours du temps)
S : personnes saines (susceptible)
E : personnes exposées non infectueuses (exposed), qui ne sont donc pas contagieuses
I : personnes infectées (infected)
R : personnes retirées (removed), guéries
avec la relation S + E + I + R = 1 (la population totale considérée, qui évolue au cours du temps)
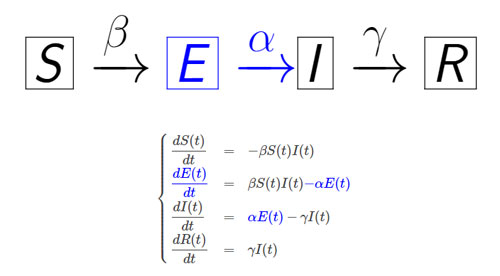
où :
β représente le taux de transmission, c’est à dire le taux de personnes saines qui deviennent infectées
α est le taux d’incubation
γ représente le taux de guérison, c’est à dire le taux de personnes infectées qui deviennent retirées
β représente le taux de transmission, c’est à dire le taux de personnes saines qui deviennent infectées
α est le taux d’incubation
γ représente le taux de guérison, c’est à dire le taux de personnes infectées qui deviennent retirées
Nota : au début de l'épidémie le taux de reproduction R0 vaut β/γ
Le modèle est amélioré en prenant en compte deux autres taux :
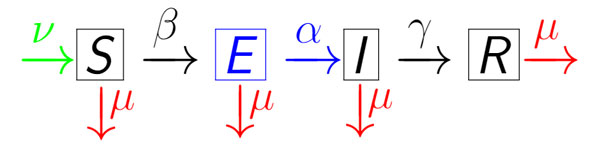
ν représente le taux de natalité de la population
μ représente le taux de mortalité de la population en général. Une personne peut décéder quelque soit son état (S,E,I ou R) et de cause non liée avec l’épidémie.
μ représente le taux de mortalité de la population en général. Une personne peut décéder quelque soit son état (S,E,I ou R) et de cause non liée avec l’épidémie.
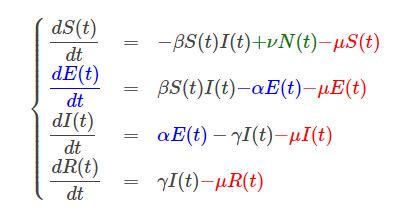
d'où le système :
La résolution numérique de ce système est très simple : les équations sont de la forme y′=f(t,y(t)), on utilise ici la méthode d’Euler qui consiste à approcher la solution y grâce à un développement de Taylor à l’ordre 1.
La solution au temps i+1 est donnée par yi+1=yi+dt.f(ti,yi), où l'évolution de chaque population au temps i+1 est calculée en fonction de l'état (connu) des populations au temps i (méthode explicite), soit :
La solution au temps i+1 est donnée par yi+1=yi+dt.f(ti,yi), où l'évolution de chaque population au temps i+1 est calculée en fonction de l'état (connu) des populations au temps i (méthode explicite), soit :

Quelques hypothèses :
- une personne retirée est immunisée
- les personnes naissent saines (R i=0=0)
- les taux α,β,γ,μ et ν sont déterminés en collaboration avec les équipes médicales, les épidémiologistes et virologistes, et les mathématiciens.
Les taux de natalité et de mortalité peuvent être obtenus sur le site de l’INSEE.
- une personne retirée est immunisée
- les personnes naissent saines (R i=0=0)
- les taux α,β,γ,μ et ν sont déterminés en collaboration avec les équipes médicales, les épidémiologistes et virologistes, et les mathématiciens.
Les taux de natalité et de mortalité peuvent être obtenus sur le site de l’INSEE.
Le cas de calcul présenté (revoir référence) m'a permis de valider le modèle.
Les taux retenus sont les suivants :
β = 0,8 (transmission)
α = 0,75 (incubation)
γ = 0,05 (guérison)
ν = 0,009 (natalité)
μ = 0,01 (mortalité)
En conditions initiales S=0,6 E=0,1 I=0,4 R=0.
Les taux retenus sont les suivants :
β = 0,8 (transmission)
α = 0,75 (incubation)
γ = 0,05 (guérison)
ν = 0,009 (natalité)
μ = 0,01 (mortalité)
En conditions initiales S=0,6 E=0,1 I=0,4 R=0.
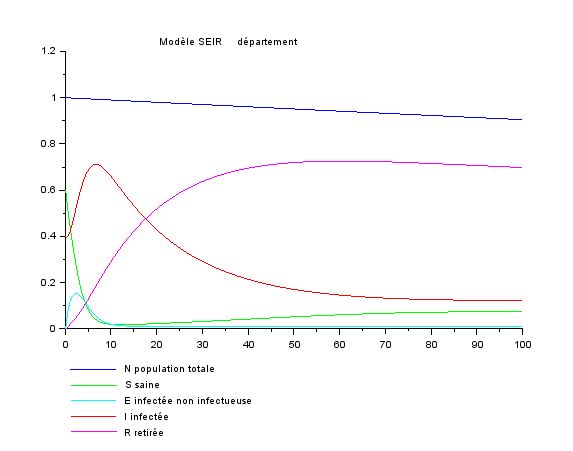
Nota : la lecture attentive de l'article m'a permis de détecter une petite erreur de transcription qui s'y était glissée ...et qui a été corrigée.
Commentaires : la population diminue car le taux de mortalité est supérieur au taux de natalité. Les courbes des personnes saines et retirées croissent dès lors que la courbe des personnes infectées commence à décroitre.
Ce modèle simplifié (beaucoup de paramètres sont occultés, en particulier l'âge) permet donc de suivre l'évolution d'une épidémie dans une population donnée.
Il manque un paramètre essentiel : l'espace.
On sait en effet, nous l'entendons chaque jour avec l'épidémie du Covid, que la diffusion d'un virus se comporte différemment d'un endroit à l'autre (ville, département, pays, ...). Savoir évaluer ce paramètre peut participer au controle de l'épidémie (confinement ciblé).
J'avais une idée en tête : il y a 95 départements en France métropolitaine (abstraction des DOM-TOM) où le virus circule. Chacun d'entre eux peut être assimilé à un modèle SEIR (avec sa population) qu'il suffit de coupler avec ses voisins par des équations adaptées.
La Corse (département 20) est conservée dans la liste pour garder la continuité numérique des 95 éléments mais une absence de coupkage traduit son isolement géographique.
La simplicité du modèle numérique permet cette approche.
Dans un premier temps j'ai identifié les k départements adjacents (limites communes) au département j [1,95]. La matrice 95x95 peut être compressée à 95xkmax en considérant la valeur max de k (kmax).
Comment exprimer les échanges entre départements qui accélérent la circulation du virus ?
La première idée est de soustraire (population S) et rajouter (population E) un terme supplémentaire équivalent à β.S(t).I(t) [S(t)I(t) représente le nombre de contacts entre des personnes saines et des personnes infectées] pour les k couplages du département j pondéré par le rapport des populations Cpopu, soit Cpopu.Sj(t).Ik(t).....
β étant le taux de transmission, Coef un coefficient arbitraire, il y a β.Coef.Cpopu.Sj(t).Ik(t) personnes nouvellement infectées dans le département j par les personnes infectées des k départements adjacents, sans transfert effectif de population d'un département à l'autre (on considère que les personnes quittent leurs k départements pour aller infecter leur voisin j et y reviennent).
Dans cette approche chaque département j a sa population Nj et peut avoir ses carctéristiques propres (taux, conditions initiales). Ici ces caractéristiques sont constantes.
Remarquons que les départements de la frontière est de la France sont artificiellement isolés dans ce modèle (pas de contact avec les pays frontaliers, soit une condition limite d'isolement).
On sait en effet, nous l'entendons chaque jour avec l'épidémie du Covid, que la diffusion d'un virus se comporte différemment d'un endroit à l'autre (ville, département, pays, ...). Savoir évaluer ce paramètre peut participer au controle de l'épidémie (confinement ciblé).
J'avais une idée en tête : il y a 95 départements en France métropolitaine (abstraction des DOM-TOM) où le virus circule. Chacun d'entre eux peut être assimilé à un modèle SEIR (avec sa population) qu'il suffit de coupler avec ses voisins par des équations adaptées.
La Corse (département 20) est conservée dans la liste pour garder la continuité numérique des 95 éléments mais une absence de coupkage traduit son isolement géographique.
La simplicité du modèle numérique permet cette approche.
Dans un premier temps j'ai identifié les k départements adjacents (limites communes) au département j [1,95]. La matrice 95x95 peut être compressée à 95xkmax en considérant la valeur max de k (kmax).
Comment exprimer les échanges entre départements qui accélérent la circulation du virus ?
La première idée est de soustraire (population S) et rajouter (population E) un terme supplémentaire équivalent à β.S(t).I(t) [S(t)I(t) représente le nombre de contacts entre des personnes saines et des personnes infectées] pour les k couplages du département j pondéré par le rapport des populations Cpopu, soit Cpopu.Sj(t).Ik(t).....
β étant le taux de transmission, Coef un coefficient arbitraire, il y a β.Coef.Cpopu.Sj(t).Ik(t) personnes nouvellement infectées dans le département j par les personnes infectées des k départements adjacents, sans transfert effectif de population d'un département à l'autre (on considère que les personnes quittent leurs k départements pour aller infecter leur voisin j et y reviennent).
Dans cette approche chaque département j a sa population Nj et peut avoir ses carctéristiques propres (taux, conditions initiales). Ici ces caractéristiques sont constantes.
Remarquons que les départements de la frontière est de la France sont artificiellement isolés dans ce modèle (pas de contact avec les pays frontaliers, soit une condition limite d'isolement).
Je présente ici les résultats de quelques simulations.
Les deux premières réalisées avec Coef=0 c'est à dire sans couplage entre départements : les résultats sont identiques pour tous, comme celui choisi au hasard (39).
Pas de temps : 0,2 (pas vraiment la dimension d'un temps car toutes les valeurs sont sans dimension)
Conditions initiales : S=0,4 I=0,2 R=0, donc E=0,4
Arrêt calcul si I<1.E-04
α=0.5, β=0.8, μ=0.095, ν=0.09
γ=0.3 et 1.
Les deux premières réalisées avec Coef=0 c'est à dire sans couplage entre départements : les résultats sont identiques pour tous, comme celui choisi au hasard (39).
Pas de temps : 0,2 (pas vraiment la dimension d'un temps car toutes les valeurs sont sans dimension)
Conditions initiales : S=0,4 I=0,2 R=0, donc E=0,4
Arrêt calcul si I<1.E-04
α=0.5, β=0.8, μ=0.095, ν=0.09
γ=0.3 et 1.
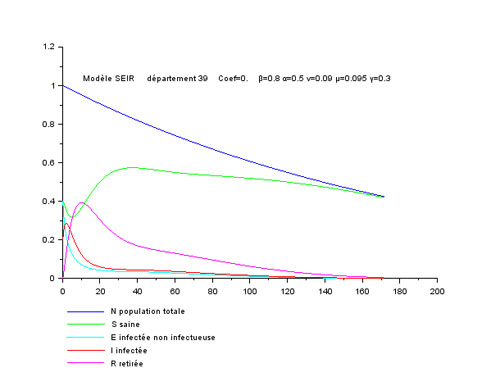
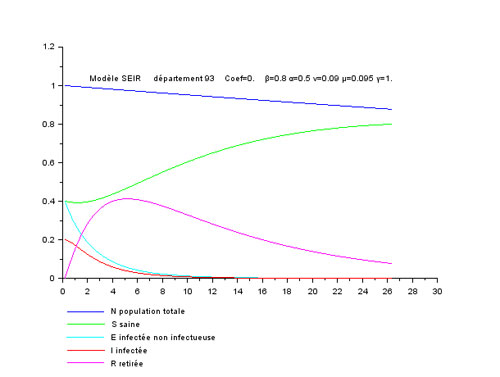
Résultats très différents avec les deux taux de guérison γ : à gauche avec un fort taux de reproduction (R0>1), à droite 100% des personnes infectées sont guéries, dans les 2 cas la population baisse (mortalité > natalité).
Maintenant les couplages entre départements sont activés avec Coef=0.4
Le taux d'infection initial n'est plus constant et égal à 0.2 mais pris égal au taux de posivité de chaque département (source non notée datant de décembre 2020).
γ=1.
Deux départements 39 et 29.
Le taux d'infection initial n'est plus constant et égal à 0.2 mais pris égal au taux de posivité de chaque département (source non notée datant de décembre 2020).
γ=1.
Deux départements 39 et 29.
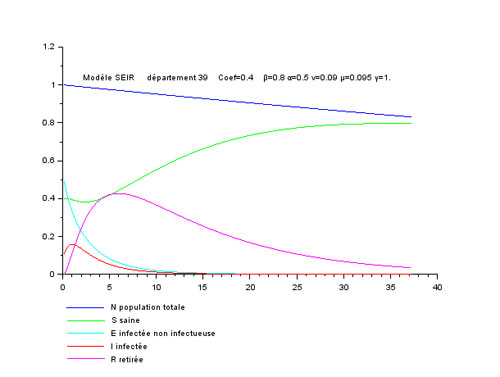
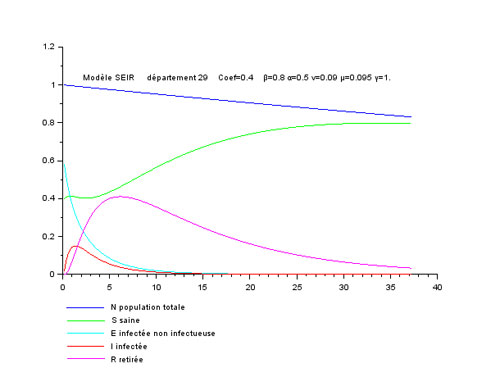
Comportements légèrement différents, surtout liés à la condition initiale différente sur I.
L'effet des couplages ne saute pas aus yeux !
L'effet des couplages ne saute pas aus yeux !
Pour montrer que ces couplages existent bien j'ai tracé la population saine S (ordonnées) en fonction des 95 départements (abscisses), à chaque temps de calcul.
Le résultat peut paraitre confus : chaque courbe représente un temps, courbe vers le haut pour les temps croissants. Mais attention la liaison entre chaque point (un point=un département) d'une courbe n'a pas de sens, ce ne sont pas les couplages réels d'un département.
Exemple : le département 50 n'est pas couplé avec le 49 et le 51 (en réalité avec les départements14, 35, 53, 61).
C'est juste une repésentation.
Comme on peut le voir, les populations saines de chaque département n'évoluent pas très différemment les unes des autres.
Le résultat peut paraitre confus : chaque courbe représente un temps, courbe vers le haut pour les temps croissants. Mais attention la liaison entre chaque point (un point=un département) d'une courbe n'a pas de sens, ce ne sont pas les couplages réels d'un département.
Exemple : le département 50 n'est pas couplé avec le 49 et le 51 (en réalité avec les départements14, 35, 53, 61).
C'est juste une repésentation.
Comme on peut le voir, les populations saines de chaque département n'évoluent pas très différemment les unes des autres.
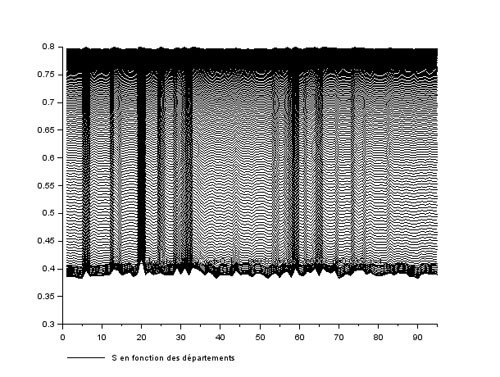
Rappelons que dans la réalité la différence dans la diffusion du virus entre l'est et l'ouest de la France pourrait être liée en partie à des critères géographiques : l'ouest est limité par l'océan, moins d'échange possible, l'est est en contact avec plusieurs pays frontaliers (Italie, Suisse, Allemagne, Luxembourg, Belgique) où la circulation de population - et du virus- est un fait (mais non prise en compte ici).
On le pressent bien : ce modèle n'est pas assez représentatif..
Il faudrait :
Il faudrait :
- différencier les taux (α,β,γ,μ et ν) par département
- prendre en compte la pyramide des âges de la population de chaque département
- différencier les populations décédées de la maladie
- ajouter une condition limite pour les départements de l'est de la france ayant une partie commune avec un des pays frontaliers.
- introduire une perte d'immunité
- quantifier l'effet d'une vaccination
- etc ...
↑ Haut de page ↑
Le 10.04.2020
Epidémiologie
Dans mon désir de vouloir absolument anticiper l'avenir, à partir des données quotidiennes en France du nombre de cas avérés, du nombre de décès, etc ... je repensais au modèle proies/prédateurs de Volterra-Lokta dont j'ai parlé ici.
Le virus prédateur contre la proie humaine ...
Sauf qu'ici le virus a un espace quasi 'inépuisable', il peut prospérer sur plus de 7 milliards d'individus et il est lui-même infini. Et pas de possibilité pour les 'proies' de se reconstituer. Du moins pas de dynamique en cycle périodique, quoique ....
Bon, c'est un peu plus compliqué.
En cherchant un peu j'ai découvert le blog d'un docteur en Mathématiques passé par l'ENS qui a abordé ce problème du calcul du nombre de personnes pouvant être infectées par une épidémie ... Les articles datent de début mars puis du 2 avril dernier.
Impressionnant, il y parle d'épidémiologie mathématique avec un modèle dit SIR, où S, I, R ≥0 sont les proportions de susceptibles (non infectés mais susceptibles de l'être), d'infectieux (infectés et infectieux) et de rétablis (guéris ou décédés) dans la population...
Ce modèle est régi par un système de 3 équations différentielles non linéaires avec l'identité S+I+R=1 (100%)
Je laisse le lecteur découvrir cette analyse. C'est passionnant ... et un peu ardu !
Le virus prédateur contre la proie humaine ...
Sauf qu'ici le virus a un espace quasi 'inépuisable', il peut prospérer sur plus de 7 milliards d'individus et il est lui-même infini. Et pas de possibilité pour les 'proies' de se reconstituer. Du moins pas de dynamique en cycle périodique, quoique ....
Bon, c'est un peu plus compliqué.
En cherchant un peu j'ai découvert le blog d'un docteur en Mathématiques passé par l'ENS qui a abordé ce problème du calcul du nombre de personnes pouvant être infectées par une épidémie ... Les articles datent de début mars puis du 2 avril dernier.
Impressionnant, il y parle d'épidémiologie mathématique avec un modèle dit SIR, où S, I, R ≥0 sont les proportions de susceptibles (non infectés mais susceptibles de l'être), d'infectieux (infectés et infectieux) et de rétablis (guéris ou décédés) dans la population...
Ce modèle est régi par un système de 3 équations différentielles non linéaires avec l'identité S+I+R=1 (100%)
Je laisse le lecteur découvrir cette analyse. C'est passionnant ... et un peu ardu !
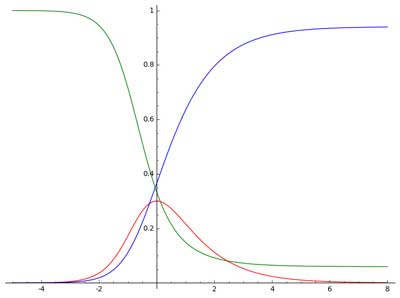
A mon humble niveau je n'en retiendrai que cette courbe bleue (indépendamment des unités) à laquelle nous devons absolument arriver ...
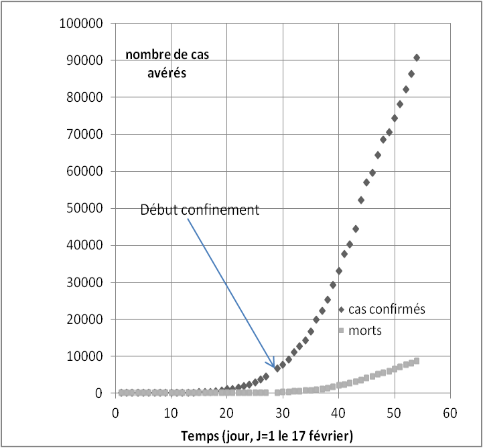
Hélas, nous n'y sommes pas encore, ce soir la courbe est encore fortement ascendante :
(Décès hors EPHAD)
Avant d'aller dormir je recommande la lecture de ces 2 articles :
- porter une regard circonspect sur l'ensemble des chiffres qui sont déversés quotidiennement et prendre un peu de recul,
- comprendre de manière ludique les stratégies envisagées pour sortir de cette crise.
↑ Haut de page ↑
Le 15.03.2020
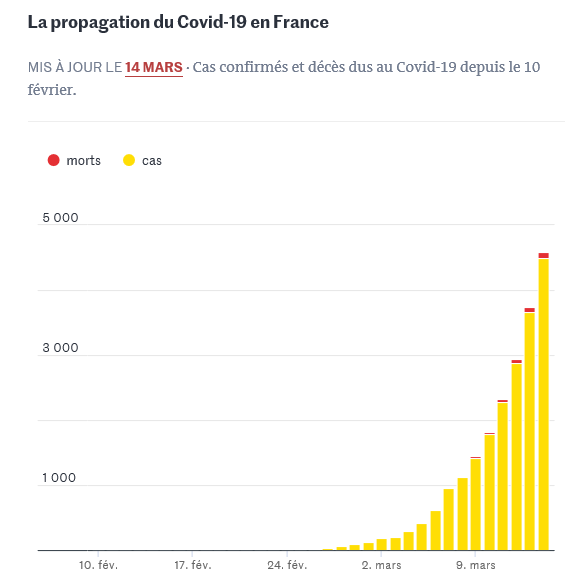
Pandémie
Extrait du journal Le Monde : la propagation de l'épidémie de coronavirus en France suit jusqu'à ce jour une courbe fortement ascendante ...
Les relévés ont débuté le 17 février (J=1)
Les relévés ont débuté le 17 février (J=1)
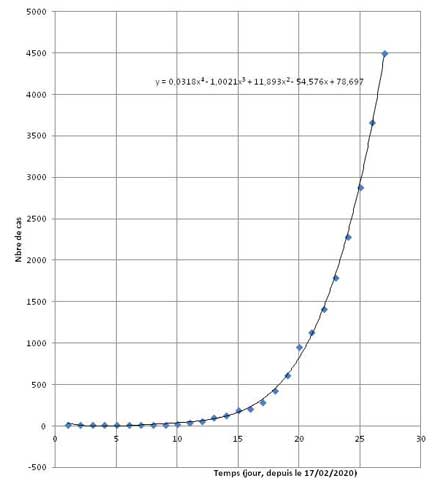
En numérisant cette coube sous excel, je peux tracer une courbe de tendance qui suit au mieux la courbe originale avec une régression polyniomiale du 4ième degré.
Une projection à J=44 (27 mars) donne ... plus de 50000 cas déclarés !
Le ministère de la santé a annoncé qu'il y avait de disponibles dans notre pays 5000 lits de réanimation et 7 364 lits dans les unités soins intensifs (Cf Le Monde], soit # 12000 lits.
A ce jour environ 12% des cas déclarés nécessitent une hospitalisation (pour pneumonie et insuffisance respiratoire).
Ce qui veut dire que si le nombre de cas déclarés dépasse 100000 (12000/12x100) les moyens de santé (techniques ... et le personnel de santé, ne les oublions pas) seront débordés !
Une projection à J=44 (27 mars) donne ... plus de 50000 cas déclarés !
Le ministère de la santé a annoncé qu'il y avait de disponibles dans notre pays 5000 lits de réanimation et 7 364 lits dans les unités soins intensifs (Cf Le Monde], soit # 12000 lits.
A ce jour environ 12% des cas déclarés nécessitent une hospitalisation (pour pneumonie et insuffisance respiratoire).
Ce qui veut dire que si le nombre de cas déclarés dépasse 100000 (12000/12x100) les moyens de santé (techniques ... et le personnel de santé, ne les oublions pas) seront débordés !
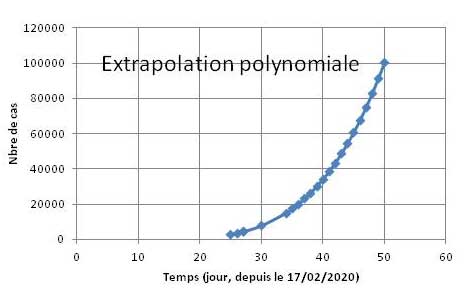
La projection polynomiale à partir de la courbe de tendance nous indique que ce chiffre pourrait être atteint (c'est une estimation) vers le 50ième jour ...soit environ le 2 avril prochain.
Ceci toutes conditions égales par ailleurs, c'est à dire avec les mesures préconisées depuis le début de la crise jusqu'à hier soir, sans conteste insuffisantes.
Ceci toutes conditions égales par ailleurs, c'est à dire avec les mesures préconisées depuis le début de la crise jusqu'à hier soir, sans conteste insuffisantes.
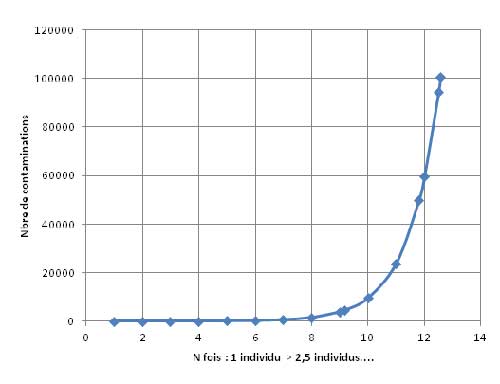
Le taux moyen de transmission est estimé à 2,5, c'est à dire que le patient 0 a pu infecter 2,5 personnes, qui ont chacune infecté 2,5 autres individus, etc. etc.
C'est une progression géométrique de raison 2,5.
La courbe ci-contre est l'illustration de cette progression.
Pour vérifier si le taux de transmission est bien de 2,5 il faudrait comparer cette courbe à celle de l'extrapolation polynomiale sur une base commune (ex : 100000 cas) en normant chacune d'elle en y/ymax et x/xmax)
C'est une progression géométrique de raison 2,5.
La courbe ci-contre est l'illustration de cette progression.
Pour vérifier si le taux de transmission est bien de 2,5 il faudrait comparer cette courbe à celle de l'extrapolation polynomiale sur une base commune (ex : 100000 cas) en normant chacune d'elle en y/ymax et x/xmax)
On peut imaginer comme l'ont fait les allemands (je fais confiance à Angela Merkel qui a une culture scientifique) que 50%, voire plus, de la population vont être porteurs du virus. Ce qui ne signifie pas que les 50% vont développer la maladie. Une bonne partie va s'auto-immuniser ...
Le délai d'incubation sur une personne infectée est de 5 à 6 jours.
Soyons en conscient : le nombre de cas graves va aller en augmentant dans les prochaines semaines, malgré les dernières mesures restrictives prises hier et aujourd'hui 15 mars...
Comment faire pour juguler cette pandémie ? Il faut réduire le taux de transmission à une valeur <1.
Que faire ? Avoir un comportement responsable et respecter les consignes ....
Le délai d'incubation sur une personne infectée est de 5 à 6 jours.
Soyons en conscient : le nombre de cas graves va aller en augmentant dans les prochaines semaines, malgré les dernières mesures restrictives prises hier et aujourd'hui 15 mars...
Comment faire pour juguler cette pandémie ? Il faut réduire le taux de transmission à une valeur <1.
Que faire ? Avoir un comportement responsable et respecter les consignes ....
↑ Haut de page ↑
Le 12.10.2017
Les jeux de hasard : correctif
J'avais oublié d'en faire mention : depuis plus d'un an la Française des Jeux a modifié le tirage de l'Euro-Millions.
Ma présentation du 09.04.2015 devait corrigée ...
Certes, quelques autres possibilités de gagner (des petites sommes) sont offertes, moyennant d'ailleurs un supplément de finance !
Mais surtout, la deuxième combinaison K voit ses nombres passer de 11 [1, ...11] à 12 [1, ... 12]
Le nombre total de combinaisons possibles (NC) est égal au produit du nombre de combinaisons de chacun des 2 tirages, Cnp et Kmq :
NC= Cnp x Kmq,
Cnp : n=50, p=5, où Cnp = n! /[p!(n-p)!], inchangée
Kmq : m=12, q=2 où Knp = m! /[q!(m-q)!]
Ce changement anodin fait passer :
K112 = 11!/[2!(11-2)!] = 11!/(2! x 9!) = (9!x10x11)/2!/9! = 10x11/2 = 55
à
K122 = 12!/[2!(12-2)!] = 12!/(2! x 10!) = (10!x11x12)/2!/10! = 11x12/2 = 66
Et donc
NC = 2118760 x 66 = 139 838 160 combinaisons possibles !
Soit une probabilité de trouver la combinaison complète gagnante de # 7,15. 10-9 !!! (<10-8)
Soit vraiment pas grand chose ...
Ma présentation du 09.04.2015 devait corrigée ...
Certes, quelques autres possibilités de gagner (des petites sommes) sont offertes, moyennant d'ailleurs un supplément de finance !
Mais surtout, la deuxième combinaison K voit ses nombres passer de 11 [1, ...11] à 12 [1, ... 12]
Le nombre total de combinaisons possibles (NC) est égal au produit du nombre de combinaisons de chacun des 2 tirages, Cnp et Kmq :
NC= Cnp x Kmq,
Cnp : n=50, p=5, où Cnp = n! /[p!(n-p)!], inchangée
Kmq : m=12, q=2 où Knp = m! /[q!(m-q)!]
Ce changement anodin fait passer :
K112 = 11!/[2!(11-2)!] = 11!/(2! x 9!) = (9!x10x11)/2!/9! = 10x11/2 = 55
à
K122 = 12!/[2!(12-2)!] = 12!/(2! x 10!) = (10!x11x12)/2!/10! = 11x12/2 = 66
Et donc
NC = 2118760 x 66 = 139 838 160 combinaisons possibles !
Soit une probabilité de trouver la combinaison complète gagnante de # 7,15. 10-9 !!! (<10-8)
Soit vraiment pas grand chose ...
↑ Haut de page ↑
Le 25.02.2017
Das Rätsel
Vu dans un cours d'allemand, prétexte à une rencontre, improbable (!), "Wer vergiftete den Meisterdetektiv ?" entre Miss Marple, Sherlock Holmes, Charlie Chan et Hercule Poirot.
Pendant le repas Charlie Chan lance un défi à Hercule Poirot :
Pendant le repas Charlie Chan lance un défi à Hercule Poirot :

... "Lieber Monsieur Poirot, da bin ich entschieden anderer Ansicht", lispelte Charlie Chan und stellte die Tischrunde gleich mit einem Zahlendenksport auf die Probe : "Schleiben Sie eine Division, indem Sie alle Ziffeln von Null bis Neun je einmal verwenden. Als Lösung muss die Zahl Sieben erscheinen" ...
Le problème posé est clair : trouver 2 nombres, les entiers M et N, composés à eux deux des 10 chiffres 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ne les utilisant qu'une seule fois et dont le quotient M/N vaut 7.
J'ai délibérément évité la voie arithmétique pure.
J'ai repris mon petit logiciel préféré de calcul numérique de toutes sortes Scilab ... et un peu de logique !
J'ai délibérément évité la voie arithmétique pure.
J'ai repris mon petit logiciel préféré de calcul numérique de toutes sortes Scilab ... et un peu de logique !
Voici la programmation qui tient en quelques lignes :

Résultat :
M=98532
N=14076
Solution unique
Durée du calcul sur un core i3 : à peine 10s pour effectuer les trois boucles principales.
A vos règles à calcul !!
M=98532
N=14076
Solution unique
Durée du calcul sur un core i3 : à peine 10s pour effectuer les trois boucles principales.
A vos règles à calcul !!
↑ Haut de page ↑
Le 07.02.2017 complèté le 21.02.2017
Echange convectif en paroi
Je reviens sur le problème soulevé dans la rubrique "Energie" concernant les différents ressentis par le corps humain en cas d'exposition au froid, en présence d'un écoulement (vent) ou non.
L'explication me laissait un gout d'inachevé ..
L'explication me laissait un gout d'inachevé ..
Regardons de nouveau ce critère de "température ressentie" tel qu'il a été décrit par ses auteurs, et qui, répétons-le, n'est pas une température, comme les médias le laissent croire.
Lecture : avec une température extérieure de -10°C, sans vent, le ressenti est de "-10". Avec vent de 30km/h il devient "-20". Etc ...
Lecture : avec une température extérieure de -10°C, sans vent, le ressenti est de "-10". Avec vent de 30km/h il devient "-20". Etc ...
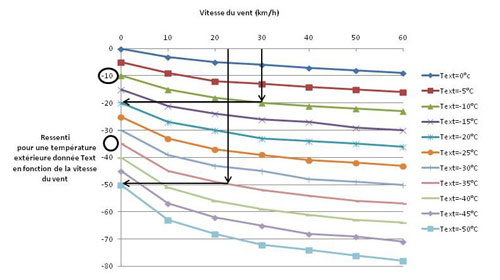
Ou, autrement dit sur un autre cas : le ressenti ("-57") est le même à Text=-45°C et vent de 10km/h qu'à Text=-35°C et vent de 60km/h.
Il faut peut-être aller voir en détail ce qu'il se passe en termes de flux de chaleur ....
Cette configuration d'échange thermique Paroi/Fluide pourrait être simplement modélisé par un modèle aux différences finies, comme ce fut le cas dans la rubrique Energie dans la comparaison PTE/PTI [1,2].
Or, coup de chance, dans une configuration approchée, l'équation de la chaleur (Fourier) a une solution analytique dont j'ai trouvé la solution ici :
Or, coup de chance, dans une configuration approchée, l'équation de la chaleur (Fourier) a une solution analytique dont j'ai trouvé la solution ici :
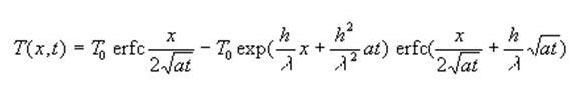
Je dis configuration approchée car il s'agit ici du cas d'un milieu semi-infini. La solution devra donc être employée avec certaines précautions (limite de validité de la solution pour la propagation du signal thermique dans un milieu fini).
Quoiqu'il en soit, la température à l'abscisse x au temps t Txt s'exprime par:
Txt = T° .ψ (x,t, h, a et λ)
Notons que dans les hypothèses Tx0 vaut zéro.
La solution normée peut donc aussi s'écrire [Txt - Tx0 ]/[T inf - Tx0] = ψ (x,t, h, a et λ)
Quoiqu'il en soit, la température à l'abscisse x au temps t Txt s'exprime par:
Txt = T° .ψ (x,t, h, a et λ)
- T° Température infinie dans le fluide (plutôt appelée Tinf en mécanique des fluides)
- h coefficient d'échange à la paroi (W/m2)
- a diffusivité du milieu solide
- λ conductivité dans le milieu solide
Notons que dans les hypothèses Tx0 vaut zéro.
La solution normée peut donc aussi s'écrire [Txt - Tx0 ]/[T inf - Tx0] = ψ (x,t, h, a et λ)
La résolution de cette équation a été réalisée avec le logiciel, extraordinaire de simplicité d'utisation, Scilab, que j'ai déjà présenté par ailleurs.
Mais avant cela, tout la difficulté réside dans l'estimation du coefficient d'échange en paroi h.
Pour cela je me suis appuyé sur quelques relations empiriques utilisées en mécanique des fluides faisant intervenir des nombres sans dimension spécifique.
Pour rappel ...
Pour cela je me suis appuyé sur quelques relations empiriques utilisées en mécanique des fluides faisant intervenir des nombres sans dimension spécifique.
Pour rappel ...
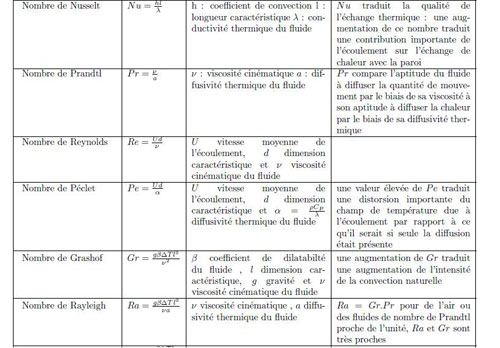
Les relations bâties à partir d'expérimentations, sont nombreuses. Celles retenues sont extraites de ce cours.
La démarche, pour qui connait un peu le sujet, est classique : calcul du nombre de Nusselt à partir de ces relations empiriques sachant par ailleurs que Nu moyen s'écrit par définition : Nu=h.L/λ, avec L longueur carcatéristique.
Deux problématiques :
Deux cas seront à examiner :
La démarche, pour qui connait un peu le sujet, est classique : calcul du nombre de Nusselt à partir de ces relations empiriques sachant par ailleurs que Nu moyen s'écrit par définition : Nu=h.L/λ, avec L longueur carcatéristique.
Deux problématiques :
- quelle longueur caractéristique L choisir ?
- faut-il considérer ici l'analogie avec la plaque plane ou celle de l'obstacle plus ou moins cylindrique en point d'arrêt ?
Deux cas seront à examiner :
- sans vent, les échanges en paroi se font par convection naturelle.
- avec vent, il s'agit de convection forcée
Convection naturelle |
Nu=f(Gr, Pr) |
Gr=g*b*DT*L3/nair2
Pr=.7 pour l’air
Si (Gr*Pr)>109) >>> régime turbulent : Nu=.13*(Gr*Pr)0.33
Si (Gr*Pr)<109) >>> régime laminaire : Nu=.677*Pr0.5*Gr0.25/(.95+Pr)0.25 |
Convection forcée | |
NU=f(Re, Pr) | |
Plaque plane | Cylindre |
Nbre de Reynolds : Re=Vent*L/nair
Si Re> 3. 105 >>> régime turbulent : Nu=.36*Pr0.33*Re0.8
Si Re< 3. 105 >>> régime laminaire (Pr>0,1) : Nu=0.664*Re0.5*Pr0.33 | Nbre de Reynolds : Re=Vent*R/nair
Si Re € [1, 0000] Nu=0.43+0.53*Pr0.31*Re0.5
Si Re € [4000, 40000] Nu=0.43+0.193*Pr0.31*Re0.618
Si Re € [40000, 400000] Nu=0.43+0.0265*Pr0.31*Re0.805 |
Dans le cas de la convection forcée, les 2 types de géométrie ont été testées mais il nous a semblé plus représentatif de retenir la géométrie cylindrique, plus proche des conditions d'exposition d'un visage ou d'une main.
Pour le milieu solide, en l'occurence la peau, je me suis inspiré des données ci-contre utilisées dans une thèse : les propriétés retenues sont celles des couches externes (cornée et cellules basales)
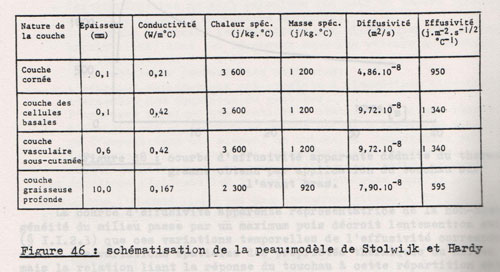
Credit Biologiedelapeau.fr
Il ne restait plus qu'à programmer la solution analytique donnée plus haut, en se donnant la possibilité de faire varier quelques paramètres et de tracer les principaux résultats [la partie code est ici pour ceux que cela intéresse].
Pour les deux cas retenus :
On notera aussi que la température normée [Txt - Tx0 ]/[T inf - Tx0] s'écrit pour ces deux cas :
Pour les deux cas retenus :
- Vent=60km/h et Vent nul, Tinf=-35°C
- Vent=10km/h et Vent nul, Tinf=-45°C
- les isochrones
- les évolutions temporelles de T en un point donné assez proche de la paroi
- les flux échangés en paroi λ.δTx=0t/dx = h.(Tx=0t - Tinf)
On notera aussi que la température normée [Txt - Tx0 ]/[T inf - Tx0] s'écrit pour ces deux cas :
- [Txt - 31 ]/[-35 - 31] soit Txt = 31 - 66.ψ (x,t, h, a et λ)
- [Txt - 31 ]/[-45 - 31] soit Txt = 31 - 76.ψ (x,t, h, a et λ
Pour ne pas alourdir cette chronique, les principaux résultats sont résumés dans le fichier suivant ...
Le lecteur attentif constatera que les résultats ne sont pas à la hauteur de ce qui était attendu !
Nous ne retrouvons pas de similitude avec les résulats des corrélations Vitesse de vent/Température extérieure, que ce soit en température (là, c'était prévisible) mais aussi en flux, loin s'en faut : comme nous l'avions écrit ici, il ne fait aucun doute que le modèle s'écarte trop de la réalité.
L'équation de Fourier dans un milieu homogène inerte et le couplage simplement convectif en paroi ne sont pas suffisants : pour un modèle plus représentatif il faudrait prendre en compte le transfert de masse dans le milieu et à sa surface (évaporation).
De fait la température Tt à un point i du milieu à l'abscisse xi est aussi fonction du débit massique (ρ variable, équation du type Arrhénius, ... ).
Et il faut rajouter en paroi, jusque dans une zone proche de la paroi, un terme modélisant le tranfert de chaleur par évaporation (chaleur latente).
Le problème se complexifie grandement car il n'est plus résolvable analytiquement.
Il faut faire appel à une méthode numérique (Différences Finies comme déjà utilisées ici, Eléments Finis) : ce pourrait être l'objet d'un prochain projet .....
Le lecteur attentif constatera que les résultats ne sont pas à la hauteur de ce qui était attendu !
Nous ne retrouvons pas de similitude avec les résulats des corrélations Vitesse de vent/Température extérieure, que ce soit en température (là, c'était prévisible) mais aussi en flux, loin s'en faut : comme nous l'avions écrit ici, il ne fait aucun doute que le modèle s'écarte trop de la réalité.
L'équation de Fourier dans un milieu homogène inerte et le couplage simplement convectif en paroi ne sont pas suffisants : pour un modèle plus représentatif il faudrait prendre en compte le transfert de masse dans le milieu et à sa surface (évaporation).
De fait la température Tt à un point i du milieu à l'abscisse xi est aussi fonction du débit massique (ρ variable, équation du type Arrhénius, ... ).
Et il faut rajouter en paroi, jusque dans une zone proche de la paroi, un terme modélisant le tranfert de chaleur par évaporation (chaleur latente).
Le problème se complexifie grandement car il n'est plus résolvable analytiquement.
Il faut faire appel à une méthode numérique (Différences Finies comme déjà utilisées ici, Eléments Finis) : ce pourrait être l'objet d'un prochain projet .....
↑ Haut de page ↑
Le 14.10.2016
Quelques notes

Je vous laisse lire l'article passionnant d'Ursula Michel sur Slate qui retrace la longue histoire du choix de la fréquence de référence du la3.
Vous le lirez, nous sommes calés aujou'hui sur le 440Hz.
Comment est venu ce choix ? Plusieurs critères ont participé à ce choix : les époques, les régions, les instruments ...
Bon, je vous l'accorde (!), quelques notions de musique seront les bienvenues ici, éventuellement avoir pratiqué quelques instruments.
A l'exemple de ma guitare électrique ci-contre (pratique en amateur de la guitare acoustique et/ou électrique depuis une quinzaine d'années)
et de mon piano (pratique pendant 6 ou 7 ans arrêtée il y a ... 50 ans mais, c'est comme le vélo, ... tout ne se perd pas !).
Vous le lirez, nous sommes calés aujou'hui sur le 440Hz.
Comment est venu ce choix ? Plusieurs critères ont participé à ce choix : les époques, les régions, les instruments ...
Bon, je vous l'accorde (!), quelques notions de musique seront les bienvenues ici, éventuellement avoir pratiqué quelques instruments.
A l'exemple de ma guitare électrique ci-contre (pratique en amateur de la guitare acoustique et/ou électrique depuis une quinzaine d'années)
et de mon piano (pratique pendant 6 ou 7 ans arrêtée il y a ... 50 ans mais, c'est comme le vélo, ... tout ne se perd pas !).

Le sujet 'musique' m'a rappelé une question que je m'étais posée il y a quelques années (question, inutile, que l'on prend le temps de se poser quand on vieillit ...)
Pourquoi 7 notes et 12 1/2 tons ?
Examinons une octave :
Do, ré, mi, fa, sol, la, si : 7 notes différentes (ensuite, répétition du cycle)
Do, do#, ré, ré#, mi, fa, fa#, sol, sol#, la, la#, si, (do) : ou plus exactement 12 sons, séparés par des ½ ton (hypothèse de base)
Notations :
Indice note : i €(1,12)
Indice octave : j €(1,8 ou 9) dans les limites des fréquences audibles et des possibilités des instruments
Comment diantre, me demandai-je, se répartissent les fréquences sur cette octave sachant que, par hypothèse, la note i de l’octave j (ki,j) a une fréquence double de la même note ki,j-1 de l’octave inférieur j-1 ?
Entre parenthèse, on peut supposer que l’idée de l’octave s’est imposée naturellement par l’harmonie à l’oreille de nos ancêtres depuis des centaines, voire des milliers d’années … ? nous verrons plus loin que c'est plus ou moins vrai.
Exercice pour petit vieux :
Soit f la fréquence.
f i,j = 2.f i,j-1 par définition de l'octave, ∀ j€(1,8 ou 9)
Soit (r) le rapport entre les 2 fréquences de 2 notes consécutives. Je suppose donc a priori qu’il existe une relation simple de proportionnalité entre ces fréquences, sinon c’est sans espoir.
f i+1,j = r.f i,j
Soit:
f 2,j = r.f 1,j
f 3,j = r.f 2,j = r2.f 1,j
……
f k,j = rk-1.f 1,j
……
f 12,j = r11.f 1,j
f 13,j = r12.f 1,j = f 1,j+1
comme f i,j+1 = 2.f i,j → 2.f 1,j = r12.f 1,j
soit r=2 1/12
r= 1,05946….
Soit donc la relation générale : f i,j = 2(i-1)/12.f 1,j
Ce rapport constant (r) entre 2 fréquences consécutives est loin d’être un nombre d’or (!), il a tout pour déplaire.
Cette démarche est purement mathématique. En l'occurence c'est une suite géométrique.
Avec cette hypothèse de proportionnalité (1/2 tons égaux) j’ai reconstruit là (par hasard) ce qu’on appelle … la gamme tempérée utilisée de nos jours.
De fait, toutes les notes, sauf le la, référencé aujourd'hui à 440Hz dit la3, et tous ses multiples et sous-multiples, qui sert au calcul de toutes les autres, auront des fréquences … pas tout à fait entières !
Bon, me voilà bien avancé.
Finalement, pas de réponse à la question pourquoi 7 notes (et 12 1/2 tons) ? Pourquoi pas 8,15, 20, ...?
Examinons une octave :
Do, ré, mi, fa, sol, la, si : 7 notes différentes (ensuite, répétition du cycle)
Do, do#, ré, ré#, mi, fa, fa#, sol, sol#, la, la#, si, (do) : ou plus exactement 12 sons, séparés par des ½ ton (hypothèse de base)
Notations :
Indice note : i €(1,12)
Indice octave : j €(1,8 ou 9) dans les limites des fréquences audibles et des possibilités des instruments
Comment diantre, me demandai-je, se répartissent les fréquences sur cette octave sachant que, par hypothèse, la note i de l’octave j (ki,j) a une fréquence double de la même note ki,j-1 de l’octave inférieur j-1 ?
Entre parenthèse, on peut supposer que l’idée de l’octave s’est imposée naturellement par l’harmonie à l’oreille de nos ancêtres depuis des centaines, voire des milliers d’années … ? nous verrons plus loin que c'est plus ou moins vrai.
Exercice pour petit vieux :
Soit f la fréquence.
f i,j = 2.f i,j-1 par définition de l'octave, ∀ j€(1,8 ou 9)
Soit (r) le rapport entre les 2 fréquences de 2 notes consécutives. Je suppose donc a priori qu’il existe une relation simple de proportionnalité entre ces fréquences, sinon c’est sans espoir.
f i+1,j = r.f i,j
Soit:
f 2,j = r.f 1,j
f 3,j = r.f 2,j = r2.f 1,j
……
f k,j = rk-1.f 1,j
……
f 12,j = r11.f 1,j
f 13,j = r12.f 1,j = f 1,j+1
comme f i,j+1 = 2.f i,j → 2.f 1,j = r12.f 1,j
soit r=2 1/12
r= 1,05946….
Soit donc la relation générale : f i,j = 2(i-1)/12.f 1,j
Ce rapport constant (r) entre 2 fréquences consécutives est loin d’être un nombre d’or (!), il a tout pour déplaire.
Cette démarche est purement mathématique. En l'occurence c'est une suite géométrique.
Avec cette hypothèse de proportionnalité (1/2 tons égaux) j’ai reconstruit là (par hasard) ce qu’on appelle … la gamme tempérée utilisée de nos jours.
De fait, toutes les notes, sauf le la, référencé aujourd'hui à 440Hz dit la3, et tous ses multiples et sous-multiples, qui sert au calcul de toutes les autres, auront des fréquences … pas tout à fait entières !
Bon, me voilà bien avancé.
Finalement, pas de réponse à la question pourquoi 7 notes (et 12 1/2 tons) ? Pourquoi pas 8,15, 20, ...?

Il faut faire un retour en arrière, jusqu'aux Ecoles Grecques (nos illustres ancêtres, 'Pythagore&Co Mannschaft ').
Là, je dois le reconnaitre, petit amateur de musique, je me suis avancé en terrain inconnu ...
Examinons la première corde (E, ou mi, même ici mi3) de la guitare ci-dessous.
Elle vibre à vide (rapport 1) entre les deux supports référencés par les 2 flèches bleues.
Si je bloque avec ma main gauche la corde exactement à mi longueur (rapport 1/2, flèche verte, même si la perspective ne le montre pas) et que je fais vibrer avec ma main droite la partie de corde restante, une certaine 'ressemblance' de son transparait avec la corde à vide.
Normal, il s'agit de la fréquence double ou octave de la note initiale (voir cours de Terminale sur les systèmes vibratoires stationnaires, noeuds et ventres, pulsations ...).
Les mathématiciens parlent d'harmonique : toute onde périodique peut toujours être décomposée en somme d'ondes "pures" (sinusoïdales) appelés harmoniques. C'est ce principe qui est utilisé dans une décomposition en série de Fourier (voir rappels ici).
Ce fut la démarche de Pythagore et de ses disciples : musique et nombres sont liés. Avec leurs critères d'harmonie les grecs recherchèrent une gamme de notes consonantes. ils construisirent une gamme dite naturelle.
Cette notion de consonance est liée au fonctionnement de l'oreille qui décompose le son en harmoniques, le cerveau reconstituant le son complet à partir de ces harmoniques. C'est pourquoi deux sons dont les harmoniques sont similaires vont paraître semblables à l'oreille. Le mélange de plusieurs sons avec des harmoniques différentes est désagréable, voire instable (phénomène dit de battement).
Cette notion de consonance peut s'exprimer ainsi :
Soit un son de fréquence fondamentale f1, un autre de fréquence fondamentale f2 : ces deux sons sont consonants si le rapport f1/f2 est un nombre rationnel (fraction d'entiers irréductibles p/q). Plus les nombres p et q sont petits, plus les deux sons ont des harmoniques en commun, et donc plus ils sont consonants.
Ce fut la démarche (intuitive) des grecs pour lesquels les premiers nombres entiers avaient une consonnance d'universalité.
Après 1/1 (la corde à vide),ils utilisèrent les rapports de fréquence 2/1 (l'octave, comme nous l'avons vu plus haut, intervalle de référence), puis 3/2 (appelé quinte), etc ... pour construire une gamme de notes consonantes.
Deux notes, c'est peu ...!
Comme le résultat entre 1 et 2/3 (3/2 en fréquence) était agréable à l'oreille, pourquoi ne pas continuer ainsi : 2/3 de la corde de longueur 2/3, soit 4/9, et ainsi de suite en suite ...
J'ai essayé d'illustrer la démarche. Pas facile facile.
On ne s'intéresse qu'à l'intervalle (octave) compris entre f et 2f, voir la figure ci-dessous :
Là, je dois le reconnaitre, petit amateur de musique, je me suis avancé en terrain inconnu ...
Examinons la première corde (E, ou mi, même ici mi3) de la guitare ci-dessous.
Elle vibre à vide (rapport 1) entre les deux supports référencés par les 2 flèches bleues.
Si je bloque avec ma main gauche la corde exactement à mi longueur (rapport 1/2, flèche verte, même si la perspective ne le montre pas) et que je fais vibrer avec ma main droite la partie de corde restante, une certaine 'ressemblance' de son transparait avec la corde à vide.
Normal, il s'agit de la fréquence double ou octave de la note initiale (voir cours de Terminale sur les systèmes vibratoires stationnaires, noeuds et ventres, pulsations ...).
Les mathématiciens parlent d'harmonique : toute onde périodique peut toujours être décomposée en somme d'ondes "pures" (sinusoïdales) appelés harmoniques. C'est ce principe qui est utilisé dans une décomposition en série de Fourier (voir rappels ici).
Ce fut la démarche de Pythagore et de ses disciples : musique et nombres sont liés. Avec leurs critères d'harmonie les grecs recherchèrent une gamme de notes consonantes. ils construisirent une gamme dite naturelle.
Cette notion de consonance est liée au fonctionnement de l'oreille qui décompose le son en harmoniques, le cerveau reconstituant le son complet à partir de ces harmoniques. C'est pourquoi deux sons dont les harmoniques sont similaires vont paraître semblables à l'oreille. Le mélange de plusieurs sons avec des harmoniques différentes est désagréable, voire instable (phénomène dit de battement).
Cette notion de consonance peut s'exprimer ainsi :
Soit un son de fréquence fondamentale f1, un autre de fréquence fondamentale f2 : ces deux sons sont consonants si le rapport f1/f2 est un nombre rationnel (fraction d'entiers irréductibles p/q). Plus les nombres p et q sont petits, plus les deux sons ont des harmoniques en commun, et donc plus ils sont consonants.
Ce fut la démarche (intuitive) des grecs pour lesquels les premiers nombres entiers avaient une consonnance d'universalité.
Après 1/1 (la corde à vide),ils utilisèrent les rapports de fréquence 2/1 (l'octave, comme nous l'avons vu plus haut, intervalle de référence), puis 3/2 (appelé quinte), etc ... pour construire une gamme de notes consonantes.
Deux notes, c'est peu ...!
Comme le résultat entre 1 et 2/3 (3/2 en fréquence) était agréable à l'oreille, pourquoi ne pas continuer ainsi : 2/3 de la corde de longueur 2/3, soit 4/9, et ainsi de suite en suite ...
J'ai essayé d'illustrer la démarche. Pas facile facile.
On ne s'intéresse qu'à l'intervalle (octave) compris entre f et 2f, voir la figure ci-dessous :
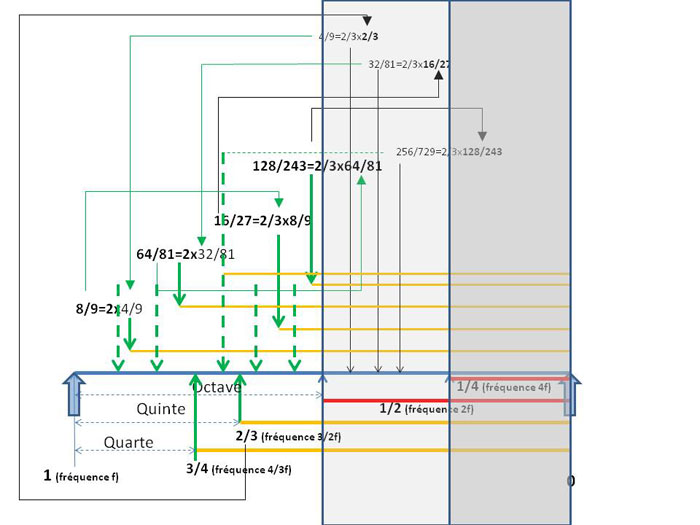
Pas de panique ...
La ligne bleue épaisse, ma corde à vide (fréquence f), la 1ère ligne rouge l'octave supérieure (2f), ...
Après avoir posé la quarte, au tour de la quinte avec 2/3 de la longueur de corde (les longueurs de corde sont représentées en jaune).
Les 2/3 de cette longueur me donnent 4/9 de corde : je suis à l'octave au-dessus. Un multiplication par 2 me ramène à mon octave initial avec une longueur de corde de 8/9.
Les 2/3 de cette longueur donne une corde de longueur 16/27. Les 2/3 de cette longueur m'amène encore à l'octave du dessus (32/81). J'obtiens 64/81 par une nouvelle multiplication par 2 dans l'octave initial. Et qui donne encore le rapport 128/243 dans cet même octave en en prenant les 2/3.
Nous avons là 7 notes (6 flèches vertes verticales trait continu) avec l'unisson (flèche bleue épaisse, rapport 1).
Faisons le lien entre gamme naturelle et gamme tempérée :
La ligne bleue épaisse, ma corde à vide (fréquence f), la 1ère ligne rouge l'octave supérieure (2f), ...
Après avoir posé la quarte, au tour de la quinte avec 2/3 de la longueur de corde (les longueurs de corde sont représentées en jaune).
Les 2/3 de cette longueur me donnent 4/9 de corde : je suis à l'octave au-dessus. Un multiplication par 2 me ramène à mon octave initial avec une longueur de corde de 8/9.
Les 2/3 de cette longueur donne une corde de longueur 16/27. Les 2/3 de cette longueur m'amène encore à l'octave du dessus (32/81). J'obtiens 64/81 par une nouvelle multiplication par 2 dans l'octave initial. Et qui donne encore le rapport 128/243 dans cet même octave en en prenant les 2/3.
Nous avons là 7 notes (6 flèches vertes verticales trait continu) avec l'unisson (flèche bleue épaisse, rapport 1).
Faisons le lien entre gamme naturelle et gamme tempérée :
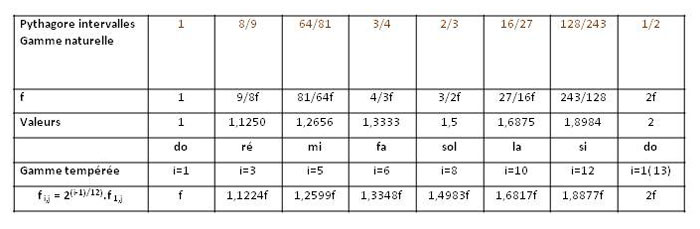
Nous pouvons remarquer un biais : les fréquences ne sont pas tout à fait identiques entre les deux gammes.
Et conséquence, pour la gamme naturelle, l'intervalle entre 2 notes de l'octave ne sera pas constant. Ce qui ne peut pas être le cas, par hypothèse, avec la gamme tempérée (voir démonstration plus haut).
Exemple, reprenons notre La3 à 440Hz.
Dans la gamme naturelle le Do inférieur se situe à 260,74 Hz (440/1,6875)
Dans la gamme tempérée ce Do vaut 261,64 Hz (440/1,6817)
Reprenons notre schéma ci-dessus avec la même logique pythagorienne, nous obtenons les 5 notes (5 flèches vertes verticales en pointillé) avec les rapports 512/729, 2048/2187, 4096/6561, 16384/19683 et 32768/59049, toujours ramenées à l'octave considérée.
Toutes ces notes s'intercalent dans celles existantes.
Par convention ces notes sont notées dièse (#) ou bémol (b).
Si on applique 12 fois l'intervalle de quinte à la note Do, on obtient un Si#, qui est presque égal à un Do, mais 7 octaves plus haut que le Do de départ et donc ... pas tout à fait un Do.
Douze quintes valent (3/2)12 # 129,7
7 octaves valent 27 # 128
Le cycle des quintes ne se referme pas, il subsiste un écart appelé "comma pythagoricien", différence entre 7 octaves et 12 quintes.
C'est pourquoi on peut se permettre de ne garder que 12 notes dans la gamme de Pythagore, si on considère que Si# est la même note que Do, que Mi# est la même note que Fa, etc...
Voilà donc pourquoi il y a 12 notes dans une octave !
Et conséquence, pour la gamme naturelle, l'intervalle entre 2 notes de l'octave ne sera pas constant. Ce qui ne peut pas être le cas, par hypothèse, avec la gamme tempérée (voir démonstration plus haut).
Exemple, reprenons notre La3 à 440Hz.
Dans la gamme naturelle le Do inférieur se situe à 260,74 Hz (440/1,6875)
Dans la gamme tempérée ce Do vaut 261,64 Hz (440/1,6817)
Reprenons notre schéma ci-dessus avec la même logique pythagorienne, nous obtenons les 5 notes (5 flèches vertes verticales en pointillé) avec les rapports 512/729, 2048/2187, 4096/6561, 16384/19683 et 32768/59049, toujours ramenées à l'octave considérée.
Toutes ces notes s'intercalent dans celles existantes.
Par convention ces notes sont notées dièse (#) ou bémol (b).
Si on applique 12 fois l'intervalle de quinte à la note Do, on obtient un Si#, qui est presque égal à un Do, mais 7 octaves plus haut que le Do de départ et donc ... pas tout à fait un Do.
Douze quintes valent (3/2)12 # 129,7
7 octaves valent 27 # 128
Le cycle des quintes ne se referme pas, il subsiste un écart appelé "comma pythagoricien", différence entre 7 octaves et 12 quintes.
C'est pourquoi on peut se permettre de ne garder que 12 notes dans la gamme de Pythagore, si on considère que Si# est la même note que Do, que Mi# est la même note que Fa, etc...
Voilà donc pourquoi il y a 12 notes dans une octave !

Chopin : valse n°10 en si mineur, opus 69 n°2, 1848
Je le reconnais, la démarche n'est pas simple et mes explications peut-être pas assez claires.
Quoiqu'il en soit, profitons de ces 12 notes, de quelque origine qu'elles soient : elles constituent le seul langage universel.
Quoiqu'il en soit, profitons de ces 12 notes, de quelque origine qu'elles soient : elles constituent le seul langage universel.
↑ Haut de page ↑
Le 13.05.2016
Différences Finies Modèle 1D
Nous avons montré les avantages d'une isolation extérieure sur un mur constitué de deux matériaux en simulant la réponse thermique de l'empilement, cas qui n'a pas de solution analytique simple.
Comment avons-nous réalisé cette simulation ?
Rappel : en monodimensionnel l’équation de diffusion de la chaleur, sans source de chaleur interne, se réduit à :
Comment avons-nous réalisé cette simulation ?
Rappel : en monodimensionnel l’équation de diffusion de la chaleur, sans source de chaleur interne, se réduit à :
δT(x,t)/δt=a.δ2T(x,t)/δx2 [0], a diffusivité du matériauAvec les hypothèses suivantes :
Condition initiale T=T0 dans les deux matériaux.Et avec les Conditions Limites (CL) (type Neumann) suivantes :
- Extérieur : flux solaire (Fs) et flux convectif (Fc) périodiques (période T)
Fs=C.sin(2.π.t/T)
C=constante W/m2Et sin(2.π.t/T) imposé à 0 si sinus négatif (pas de flux solaire pour une ½ période correspondant à la nuit)
Fc=he.(Tpext(t)-Te(t)) aveche=donné en W/m2/°CTpext(t) : inconnue, température de paroi du mur coté extérieurTe(t)=Tinit+ΔT0.sin(2.π.t/T), T extérieureTinit et ΔT0 donnésLa température Te varie sinusoïdalement de ΔT0 autour de la valeur moyenne Tinit.Dans notre hypothèse, on notera que les deux flux périodiques sont synchrones : dans la réalité la température extérieure peut encore évoluer (inertie du sol) alors que le soleil est déjà couché. Pour la démonstration l’hypothèse retenue est suffisante, mais le déphasage des deux sources pourrait être facilement réalisé …
- Intérieur : flux (Frc) radiato-convectif
Frc=(hc+hr)(Ti-Tpint(t))Ti donnée (température imposée dans la pièce)Tpint(t) : inconnue, température de paroi du mur coté intérieurhc donné en W/m2/°Chr=4.ε.σ.Ti3, linéarisation du flux radiatif échangé entre parois en considérant que Ti voisin de Tpintε : émissivité, prise égale à 1σ : constante de Stefan : 5,67.10-8 W/m2/K4
Le principe consiste à approcher la solution du problème par une approximation numérique.
L'équation est discrétisée à l’aide des Différences Finies qui sont basées sur les développements en série de Taylor (au second ordre en x, au premier ordre en t), en utilisant ici le schéma explicite (Laplacien développé au temps t) avec l’utilisation du nœud fictif en paroi.
L’avantage de cette méthode réside dans la simplicité de sa résolution, directe, avec toutefois un critère de convergence à respecter (a.dt/dx2 < ½).
L'équation est discrétisée à l’aide des Différences Finies qui sont basées sur les développements en série de Taylor (au second ordre en x, au premier ordre en t), en utilisant ici le schéma explicite (Laplacien développé au temps t) avec l’utilisation du nœud fictif en paroi.
L’avantage de cette méthode réside dans la simplicité de sa résolution, directe, avec toutefois un critère de convergence à respecter (a.dt/dx2 < ½).
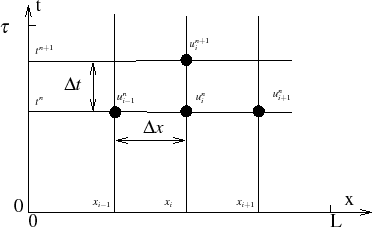
credit www.ufrmeca.univ-lyon1.fr
Signalons au passage que l'utilisation des Différences Finies (DF) a fait l'objet de centaines de publications dans différents domaines depuis cinquante ans : le lecteur curieux pourra le vérifier sur Internet où il trouvera, n'en doutons pas, les réponses à ses questions ...
Pour cette raison nous irons directement dans le vif du sujet : le Domaine de calcul en espace est discrétisé en N intervalles réguliers.
Le premier terme de notre équation [0] au noeud i s'écrit :
Cette relation permet de calculer explicitement la solution au temps t+Δt au noeud i en fonction de la solution au temps t, pour tout i ϵ [2,N-1].
Pour les noeuds en parois, il faut utiliser les Conditions Limites. Elles sont introduites ici en utilisant un noeud fictif :
Pour cette raison nous irons directement dans le vif du sujet : le Domaine de calcul en espace est discrétisé en N intervalles réguliers.
Le premier terme de notre équation [0] au noeud i s'écrit :
δT/δt it # (Ti t+Δt - Ti t)/Δt, [1] approximation d'ordre 1
Le Laplacien de la même équation est approximé par :
δ2T/δx2 # (Ti+1 t - 2.Ti t + Ti-1 t )/Δx2, approximation du second ordreSoit après remplacement :
(Ti t+Δt - Ti t)/Δt = a.(Ti+1 t - 2.Ti t + Ti-1 t )/Δx2et au final :
Ti t+Δt = Ti t + k. (Ti+1 t - 2.Ti t + Ti-1 t ) [2], avec k=a.Δt/Δx2
Cette relation permet de calculer explicitement la solution au temps t+Δt au noeud i en fonction de la solution au temps t, pour tout i ϵ [2,N-1].
Pour les noeuds en parois, il faut utiliser les Conditions Limites. Elles sont introduites ici en utilisant un noeud fictif :
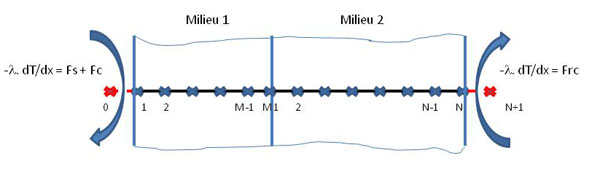
Quelque soit t :
Pour l'interface entre les deux milieux (1 et 2) pour lequel on considère un contact parfait (pas de résistance thermique), quelque soit t : Tint milieu 1 = Tint milieu 2 [3]
La solution passe par un petit algorithme utilisant les relations liants les noeuds entre eux.
Le schéma explicite utilisé est le plus simple à résoudre : il suffit de calculer T1t+Δt avec [2'], puis les températures Tt+Δt dans la premier milieu [2], Tt+Δt au contact [3], Tt+Δt dans le second milieu [2] et enfin la température TNt+Δt avec [2'']. Puis d'incrémenter le temps d'un pas de temps Δt.
A l'époque de la préhistoire (1975-1995) j'ai (beaucoup) pratiqué la programmation (Fortran, Basic, C, ..).
Mais aujourd'hui comment faire à partir de mon portable ? Quel langage ? Quel logiciel ?
Tout à fait par hasard j'ai découvert le logiciel SCILAB.
Ce logiciel libre est un logiciel de calcul numérique qui dispose de nombreuses fonctionnalités, en particulier un module de programmation, et qui offre de nombreuses possibilités pour des activités mathématiques et/ou scientifiques dans des domaines variés.
Et d'une utilisation très simple. Il m'a fallu à peine une heure pour en prendre la mesure. Mais je n'en ai pas encore utilisé 1% !
C'est un outil très puissant que je recommanderai.
Il présente plusieurs fenêtres avec un explorateur de fichiers, une zone de saisie de commande (console), un éditeur de fichier (.sci), un historique de commandes et un navigateur de variables (les variables d'un programme sont accessibles à tout moment).
Le logicilel possède son propre langage de programmation (orienté calcul numérique) qui me fait penser, pour ce que j'en ai utilisé, au BASIC de ma jeunesse, mais il peut aussi exécuter du Fortran ou du C.
Bref, les équations [1 à 3] se sont transformées en quelque lignes de code dont un extrait est présenté ci-dessous à titre indicatif, pour le coeur du calcul qui nous intéresse :
-λ.(T2-T0)/2/dx = Fs(t)+ Fc(t)
-λ.(TN+1-TN-1)/2/dx = Frc
A chaque limite du domaine, T0 et TN+1 peuvent s'écrire en fonction respectivement de T2 et de TN-1, et la relation [2] devient pour ces cas particuliers :
T1t+Δt = T1t + 2.k. (T2t - T1t) + 2.k.Δx.(Fs+Fc)/λ [2']
TNt+Δt = TNt + 2.k. (TN-1t - TNt) - 2.k.Δx.Frc/λ [2'']
Pour l'interface entre les deux milieux (1 et 2) pour lequel on considère un contact parfait (pas de résistance thermique), quelque soit t : Tint milieu 1 = Tint milieu 2 [3]
La solution passe par un petit algorithme utilisant les relations liants les noeuds entre eux.
Le schéma explicite utilisé est le plus simple à résoudre : il suffit de calculer T1t+Δt avec [2'], puis les températures Tt+Δt dans la premier milieu [2], Tt+Δt au contact [3], Tt+Δt dans le second milieu [2] et enfin la température TNt+Δt avec [2'']. Puis d'incrémenter le temps d'un pas de temps Δt.
A l'époque de la préhistoire (1975-1995) j'ai (beaucoup) pratiqué la programmation (Fortran, Basic, C, ..).
Mais aujourd'hui comment faire à partir de mon portable ? Quel langage ? Quel logiciel ?
Tout à fait par hasard j'ai découvert le logiciel SCILAB.
Ce logiciel libre est un logiciel de calcul numérique qui dispose de nombreuses fonctionnalités, en particulier un module de programmation, et qui offre de nombreuses possibilités pour des activités mathématiques et/ou scientifiques dans des domaines variés.
Et d'une utilisation très simple. Il m'a fallu à peine une heure pour en prendre la mesure. Mais je n'en ai pas encore utilisé 1% !
C'est un outil très puissant que je recommanderai.
Il présente plusieurs fenêtres avec un explorateur de fichiers, une zone de saisie de commande (console), un éditeur de fichier (.sci), un historique de commandes et un navigateur de variables (les variables d'un programme sont accessibles à tout moment).
Le logicilel possède son propre langage de programmation (orienté calcul numérique) qui me fait penser, pour ce que j'en ai utilisé, au BASIC de ma jeunesse, mais il peut aussi exécuter du Fortran ou du C.
Bref, les équations [1 à 3] se sont transformées en quelque lignes de code dont un extrait est présenté ci-dessous à titre indicatif, pour le coeur du calcul qui nous intéresse :
//-----------------------------------------------------------------------------
//milieu 1 1er noeud
Tstar1(1)=(Cs*perc+he*(Tinit+dT0*per))*2*k1*dx1/lamb1
Tstar1(1)=Tstar1(1)+TT1(1)*(1.-2*k1*(1+dx1*he/lamb1))
Tstar1(1)=Tstar1(1)+2*k1*TT1(2)
//milieu 1 2<i<N-1
for i=2:N-1
Tstar1(i)=TT1(i)+k1*(TT1(i+1)-2*TT1(i)+TT1(i-1))
end
// milieu 1 noeud N
Tstar1(N)=Tstar1(N-1)*lamb1/dx1+Tstar2(2)*lamb2/dx2
Tstar1(N)=Tstar1(N)*dx1/(lamb1+lamb2)
//-----------------------------------------------------------------------------
//milieu 1 1er noeud
Tstar1(1)=(Cs*perc+he*(Tinit+dT0*per))*2*k1*dx1/lamb1
Tstar1(1)=Tstar1(1)+TT1(1)*(1.-2*k1*(1+dx1*he/lamb1))
Tstar1(1)=Tstar1(1)+2*k1*TT1(2)
//milieu 1 2<i<N-1
for i=2:N-1
Tstar1(i)=TT1(i)+k1*(TT1(i+1)-2*TT1(i)+TT1(i-1))
end
// milieu 1 noeud N
Tstar1(N)=Tstar1(N-1)*lamb1/dx1+Tstar2(2)*lamb2/dx2
Tstar1(N)=Tstar1(N)*dx1/(lamb1+lamb2)
//-----------------------------------------------------------------------------
//milieu 2 1er noeud
Tstar2(1)=Tstar1(N)
// milieu 2 2<i<M-1
for i=2:M-1
if i==2 then
Tstar2(i)=TT2(i)+k2*(TT2(i+1)-2*TT2(i)+TT1(N))
else
Tstar2(i)=TT2(i)+k2*(TT2(i+1)-2*TT2(i)+TT2(i-1))
end
end
//milieu 2 noeud M
hr=4.*sigma*(Tint+273.)^3
htot=hc+hr
Tstar2(M)=TT2(M)*(1.-2*k2*(1.+dx2/lamb2*htot))
Tstar2(M)=Tstar2(M)+2*k2*TT2(M-1)+2*k2*dx2*Tint*htot/lamb2
Tstar2(1)=Tstar1(N)
// milieu 2 2<i<M-1
for i=2:M-1
if i==2 then
Tstar2(i)=TT2(i)+k2*(TT2(i+1)-2*TT2(i)+TT1(N))
else
Tstar2(i)=TT2(i)+k2*(TT2(i+1)-2*TT2(i)+TT2(i-1))
end
end
//milieu 2 noeud M
hr=4.*sigma*(Tint+273.)^3
htot=hc+hr
Tstar2(M)=TT2(M)*(1.-2*k2*(1.+dx2/lamb2*htot))
Tstar2(M)=Tstar2(M)+2*k2*TT2(M-1)+2*k2*dx2*Tint*htot/lamb2
Le modèle numérique étant réalisé, il peut se décliner, moyennant quelques adaptations, en de multiples versions : murs multi-couches, autres CL, ...
Le lecteur intéressé par ce type de calcul peut me contacter.
Le schéma pourrait être aussi améliorer en passant à un schéma implicite, typiquement Cranck-Nicolson inconditionnellement stable mais un peu plus difficile à mettre en oeuvre ...
Nous verrons cela pour d'autres applications !
Les résultats du modèle sont présentés à la page Energie ....
Le lecteur intéressé par ce type de calcul peut me contacter.
Le schéma pourrait être aussi améliorer en passant à un schéma implicite, typiquement Cranck-Nicolson inconditionnellement stable mais un peu plus difficile à mettre en oeuvre ...
Nous verrons cela pour d'autres applications !
Les résultats du modèle sont présentés à la page Energie ....
Nota : la vérification de la programmation a fait l'objet d'une petite validation sur un cas connu.
Les conditions limites sont réduites à :
T=10°C, imposée constante à l'extérieur
T=20°C, imposée constante à l'intérieur
(pas de coefficient d'échange en paroi)
A l'état initilal, T=10°C dans les deux matériaux (cas IC).
Le calcul converge vers le régime permanent.
En fin de calcul, le gradient dans chaque milieu :
Φ # 1,72W/m2 dans les deux milieux.
Les conditions limites sont réduites à :
T=10°C, imposée constante à l'extérieur
T=20°C, imposée constante à l'intérieur
(pas de coefficient d'échange en paroi)
A l'état initilal, T=10°C dans les deux matériaux (cas IC).
Le calcul converge vers le régime permanent.
En fin de calcul, le gradient dans chaque milieu :
- 9,878°C (isolant)
- 0,122°C (béton)
Φ # 1,72W/m2 dans les deux milieux.
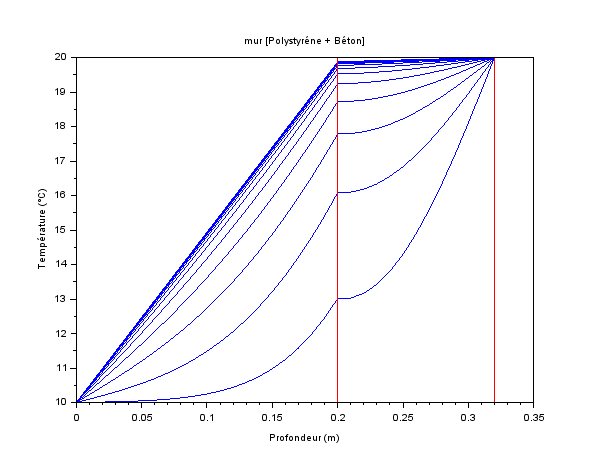
↑ Haut de page ↑
Le 25.03.2016
La Loi de Moore : la fin ?
C’est officiel : les industriels des semi-conducteurs "abandonnent" la loi de MOORE, qui a quand même été vérifiée, bon an mal an, depuis le milieu des années 60 jusqu’en 2015.
Un petit rappel : cette loi empirique, mise en évidence par Gordon Moore (qui deviendra co-fondateur d’INTEL) à partir de ses analyses, prédisait en quelque sorte l’évolution de la technologie des transistors.
Que dit cette loi : la densité de transistors gravés sur les puces des circuits des ordinateurs double et doublera tous les deux ans.
Ce constat est illustré et vérifié par la courbe ci-contre (cf Nature).
Aujourd’hui cette loi n’est plus le fil d’Ariane : jusqu’à présent les applications suivaient les améliorations des puces, maintenant les circuits intégrés iront au juste besoin que ce soit des smartphones ou des superordinateurs.
Les objectifs de miniaturisation ont porté leur fruit et ont permis le développement des machines que nous connaissons aujourd’hui.
Les problèmes thermiques apparus lorsque l’échelle des quelques dizaines de nm a été atteinte ont été résolus par des subterfuges : augmentation des fréquences d’horloge, du nombre de processeurs (plusieurs couramment aujourd’hui dans les PC et les smartphones …) mais la parallélisation a ses limites dans certains processus.
La croissance exponentielle du nombre de composants par unité de surface ne peut plus continuer car des effets quantiques entrent en jeu qui complexifient les solutions techniques
D’autres voies restent à explorer : le calculateur quantique ou optique ou encore de nouveaux matériaux (ex graphène 2D) qui s’intéresseraient au spin électronique plutôt qu’au déplacement des électrons.
En réalité, la fin annoncée de la loi de Moore est plus une question économique que technique. La construction de nouvelles chaines de fabrication photolitographiques exige des investissements de plusieurs milliards de $.
Et puis la donne a changé : les applications mobiles et les données ont migré vers des « fermes » de serveurs (cloud) qui dominent le marché pour les microprocesseurs puissants. Cette spécialisation sape le marché et pose problème aux fabricants : moins d’espoir de vendre en grand nombre.
D’où l’idée de multiplier les propositions vers le public (ce que j’appellerai créer des besoins, exemple type la tablette).
Un petit rappel : cette loi empirique, mise en évidence par Gordon Moore (qui deviendra co-fondateur d’INTEL) à partir de ses analyses, prédisait en quelque sorte l’évolution de la technologie des transistors.
Que dit cette loi : la densité de transistors gravés sur les puces des circuits des ordinateurs double et doublera tous les deux ans.
Ce constat est illustré et vérifié par la courbe ci-contre (cf Nature).
Aujourd’hui cette loi n’est plus le fil d’Ariane : jusqu’à présent les applications suivaient les améliorations des puces, maintenant les circuits intégrés iront au juste besoin que ce soit des smartphones ou des superordinateurs.
Les objectifs de miniaturisation ont porté leur fruit et ont permis le développement des machines que nous connaissons aujourd’hui.
Les problèmes thermiques apparus lorsque l’échelle des quelques dizaines de nm a été atteinte ont été résolus par des subterfuges : augmentation des fréquences d’horloge, du nombre de processeurs (plusieurs couramment aujourd’hui dans les PC et les smartphones …) mais la parallélisation a ses limites dans certains processus.
La croissance exponentielle du nombre de composants par unité de surface ne peut plus continuer car des effets quantiques entrent en jeu qui complexifient les solutions techniques
D’autres voies restent à explorer : le calculateur quantique ou optique ou encore de nouveaux matériaux (ex graphène 2D) qui s’intéresseraient au spin électronique plutôt qu’au déplacement des électrons.
En réalité, la fin annoncée de la loi de Moore est plus une question économique que technique. La construction de nouvelles chaines de fabrication photolitographiques exige des investissements de plusieurs milliards de $.
Et puis la donne a changé : les applications mobiles et les données ont migré vers des « fermes » de serveurs (cloud) qui dominent le marché pour les microprocesseurs puissants. Cette spécialisation sape le marché et pose problème aux fabricants : moins d’espoir de vendre en grand nombre.
D’où l’idée de multiplier les propositions vers le public (ce que j’appellerai créer des besoins, exemple type la tablette).
Oui, la loi de Moore se trouve face à un mur dans sa définition originale.
Elle peut renaitre en changeant son paradigme, doubler le nombre d’utilisateurs tous les deux ans, ce qui est envisageable tant que l’industrie sera capable de proposer des objets autonomes avec de nouvelles fonctionnalités, compatibles entre eux, communicant entre eux avec un niveau de sécurité élevé.
Elle l’a déjà fait.
Jusqu’à quand ?
Elle peut renaitre en changeant son paradigme, doubler le nombre d’utilisateurs tous les deux ans, ce qui est envisageable tant que l’industrie sera capable de proposer des objets autonomes avec de nouvelles fonctionnalités, compatibles entre eux, communicant entre eux avec un niveau de sécurité élevé.
Elle l’a déjà fait.
Jusqu’à quand ?
↑ Haut de page ↑
Le 25.07.2015
Bonne résolution et compression

Partons de cette photo quelque part en France (plutôt vers la Fin de la Terre !)…
La capacité théorique maximum du capteur de l’appareil utilisé (Lumix DMC FZ28 de Panasonic en l’occurrence) est de 10 700 000 pixels (~10Mpx).
Certes les constructeurs font aujourd’hui largement mieux (40Mpixels) mais nous verrons plus loin ce qu'il en est ...
Le format 3:2 ayant été sélectionné sur l’appareil, la taille maxi de l’image est restreinte à 3648x2431 pixels soit 8 868 288 pixels. (Une petite partie de la zone active du capteur n’est donc pas utilisée).
L’image a été enregistrée au format jpeg, format par défaut de l'appareil.
Pour pouvoir l'insérer ci-contre de manière non ostentatoire, l'ensemble de l'image à été réduite à 500x333 pixels.
La capacité théorique maximum du capteur de l’appareil utilisé (Lumix DMC FZ28 de Panasonic en l’occurrence) est de 10 700 000 pixels (~10Mpx).
Certes les constructeurs font aujourd’hui largement mieux (40Mpixels) mais nous verrons plus loin ce qu'il en est ...
Le format 3:2 ayant été sélectionné sur l’appareil, la taille maxi de l’image est restreinte à 3648x2431 pixels soit 8 868 288 pixels. (Une petite partie de la zone active du capteur n’est donc pas utilisée).
L’image a été enregistrée au format jpeg, format par défaut de l'appareil.
Pour pouvoir l'insérer ci-contre de manière non ostentatoire, l'ensemble de l'image à été réduite à 500x333 pixels.
Comment est défini le pixel ? C’est la plus petite partie du capteur photo sensible équipant l’appareil photo numérique. Aujourd’hui la résolution tutoie le μm.
La puce électronique qui se trouve dans l’appareil photo forme une matrice constituée de ces millions d'éléments
Deux types de technologie pour le capteur, voir liens pour plus d'informations :
La puce électronique qui se trouve dans l’appareil photo forme une matrice constituée de ces millions d'éléments
Deux types de technologie pour le capteur, voir liens pour plus d'informations :
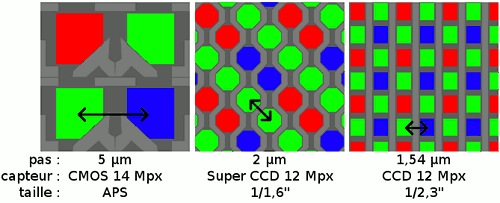
Credit lesnumeriques.com
Pour l'appareil utilisé, le capteur est du type CCD 1/2,33", avec une surface utile de 6,08mm x 4,56mm, ce qui fait un pixel d'environ 1,7 μm.
Pour faire une comparaison, le pixel, unité indivisible, est à la photo numérique ce que la molécule de bromure d'argent (AgBr) était à la photo argentique.
La résolution d'une image obtenue à l'aide d'un film argentique (réaction chimique à l’échelle de l’atome) peut être encore supérieure, pour les appareils haut de gamme, à celle des meilleurs appareils photographiques numériques mais cela ne durera pas …
Les halogénures d'argent cristallisent dans un système cubique, avec une maille de 0,5774 nm pour le bromure et 0,5550 nm pour le chlorure
En réalité le cristal présente des défauts de structure qui deviennent les pièges à électrons. L'épaisseur de l'émulsion d'un film argentique est # 25 μm. La sensibilité dépend de la taille des grains or les cristaux varient entre 0,05 μm et 1 μm ...
Nous sommes donc dans les mêmes ordres de grandeur entre numérique et argentique.
Pour les passionnés de chimie des matériaux ...
Pour faire une comparaison, le pixel, unité indivisible, est à la photo numérique ce que la molécule de bromure d'argent (AgBr) était à la photo argentique.
La résolution d'une image obtenue à l'aide d'un film argentique (réaction chimique à l’échelle de l’atome) peut être encore supérieure, pour les appareils haut de gamme, à celle des meilleurs appareils photographiques numériques mais cela ne durera pas …
Les halogénures d'argent cristallisent dans un système cubique, avec une maille de 0,5774 nm pour le bromure et 0,5550 nm pour le chlorure
En réalité le cristal présente des défauts de structure qui deviennent les pièges à électrons. L'épaisseur de l'émulsion d'un film argentique est # 25 μm. La sensibilité dépend de la taille des grains or les cristaux varient entre 0,05 μm et 1 μm ...
Nous sommes donc dans les mêmes ordres de grandeur entre numérique et argentique.
Pour les passionnés de chimie des matériaux ...

Revenons à notre photo d'origine ...
Ici l’image est une matrice de 3648 points horizontaux par 2431 points verticaux.
Chaque point est caractérisé par une intensité lumineuse qui peut être discriminée suivant une échelle allant du plus foncé (noir) au plus clair (blanc).
En utilisant le codage binaire sur 8 bits (chaque bit prenant la valeur 0 ou 1) ou un octet, il est possible de distinguer 256 niveaux différents :
00000000 (0), 00000001 (1), 00000010 (2), 00000011 (3), …, 11111110 (254), 11111111 (255).
Les 256 niveaux identifiés ci-dessus le sont sur une échelle de gris. L’image étant en couleur, chaque pixel doit être caractérisé par chacune des couleurs, rouge, vert et bleue (système RGB en anglais).
Chaque couleur est codée sur 1 octet, 3 octets sont donc nécessaires pour chaque pixel.
L’image occuperait donc une place théorique de 3x8868288 octets, > 25Mo !
Or mon image, sous le format JPEG, n’occupe que …. 4,13 Mo. Soit plus de 6 fois moins.
Qu’en est-il ?
Le format JPEG, comme tous les formats d’archivage de données numériques (GIF, PNG, …), utilise un algorithme de compression d’information, ce qui permet de réduire de manière sensible la taille de l’objet.
Les différents types de sauvegardes : avec ou sans compression, avec ou sans perte d’information.
• Sans perte : PSD (spécifique Photoshop), GIF, PNG, TIFF (sans compression)
• Avec perte : JPEG, TIFF (avec compression)
Je n’entrerai pas dans le détail de ces approches qui font appel à des notions mathématiques assez complexes : transformation de Fourier, statistiques, application de la théorie des ondelettes (fonction introduite par A. Haar en 1909 puis largement enrichie par des chercheurs français), plus récemment les fractales, etc
Le lecteur curieux et (très) avisé pourra lire cet article.
L'approche la plus basique qui vient à l’esprit : j’ai une ligne horizontale de pixels, sur celle-ci les pixels n° 35 à 200 sont quasi identiques (paysages stratifiés types bord de mer), plutôt que de coder 166 fois la même information je peux coder cette information de pixel une fois et coder les deux informations de rang (n°35 et n°200), soit 3 informations au lieu de 166.
Simplification à l'extrême mais illustration de l’esprit de la compression.
A noter donc, l'efficacité de la compression peut être très liée à la structure de l'image.
Ici l’image est une matrice de 3648 points horizontaux par 2431 points verticaux.
Chaque point est caractérisé par une intensité lumineuse qui peut être discriminée suivant une échelle allant du plus foncé (noir) au plus clair (blanc).
En utilisant le codage binaire sur 8 bits (chaque bit prenant la valeur 0 ou 1) ou un octet, il est possible de distinguer 256 niveaux différents :
00000000 (0), 00000001 (1), 00000010 (2), 00000011 (3), …, 11111110 (254), 11111111 (255).
Les 256 niveaux identifiés ci-dessus le sont sur une échelle de gris. L’image étant en couleur, chaque pixel doit être caractérisé par chacune des couleurs, rouge, vert et bleue (système RGB en anglais).
Chaque couleur est codée sur 1 octet, 3 octets sont donc nécessaires pour chaque pixel.
L’image occuperait donc une place théorique de 3x8868288 octets, > 25Mo !
Or mon image, sous le format JPEG, n’occupe que …. 4,13 Mo. Soit plus de 6 fois moins.
Qu’en est-il ?
Le format JPEG, comme tous les formats d’archivage de données numériques (GIF, PNG, …), utilise un algorithme de compression d’information, ce qui permet de réduire de manière sensible la taille de l’objet.
Les différents types de sauvegardes : avec ou sans compression, avec ou sans perte d’information.
• Sans perte : PSD (spécifique Photoshop), GIF, PNG, TIFF (sans compression)
• Avec perte : JPEG, TIFF (avec compression)
Je n’entrerai pas dans le détail de ces approches qui font appel à des notions mathématiques assez complexes : transformation de Fourier, statistiques, application de la théorie des ondelettes (fonction introduite par A. Haar en 1909 puis largement enrichie par des chercheurs français), plus récemment les fractales, etc
Le lecteur curieux et (très) avisé pourra lire cet article.
L'approche la plus basique qui vient à l’esprit : j’ai une ligne horizontale de pixels, sur celle-ci les pixels n° 35 à 200 sont quasi identiques (paysages stratifiés types bord de mer), plutôt que de coder 166 fois la même information je peux coder cette information de pixel une fois et coder les deux informations de rang (n°35 et n°200), soit 3 informations au lieu de 166.
Simplification à l'extrême mais illustration de l’esprit de la compression.
A noter donc, l'efficacité de la compression peut être très liée à la structure de l'image.
Sur cette image JPEG, il est intéressant de noter que malgré une compression avec perte (taille théorique ≠ taille réelle du fichier), l'image affichée conserve sa résolution initiale (3648x2431 pixels). Ceci se vérifie en zoomant sur l'image, exemple à l'avant du bateau.
Ici le principe de compression est fondé sur le fait que l'œil est moins sensible aux changements subtils de couleurs qu'aux variations de luminosité. Plutôt que perdre en résolution, on préfère réduire le nombre de couleurs.
Ce choix sur la perte ou non de résolution dépend énomément ... de l'utilisation qui sera faite de la photo, en particulier du support sur lequel l'image sera affichée (écran, papier, ...) et de l'interprétation qui en sera faite par l'oeil !
Ce point est fondamental.
Ainsi ma photo insérée en haut de cette rubrique réduite à 500x333 pixels est passée (de manière irréversible) d'une densité de 180 pixels/pouce à 72 pixels/pouce (fichier de 12,4ko). Mais l'impression visuelle à l'écran reste acceptable.
Ce choix sur la perte ou non de résolution dépend énomément ... de l'utilisation qui sera faite de la photo, en particulier du support sur lequel l'image sera affichée (écran, papier, ...) et de l'interprétation qui en sera faite par l'oeil !
Ce point est fondamental.
Ainsi ma photo insérée en haut de cette rubrique réduite à 500x333 pixels est passée (de manière irréversible) d'une densité de 180 pixels/pouce à 72 pixels/pouce (fichier de 12,4ko). Mais l'impression visuelle à l'écran reste acceptable.
Le besoin en résolution de l'image est donc toujours à mettre en balance avec le moyen d'affichage et les capacités discriminantes de l'oeil. Il s'agit toujours d'un compromis.
L’acuité visuelle habituellement considérée comme "normale" correspond à un angle minimum de résolution d’environ 1 minute d’arc (1/60e de degré d’angle visuel).
Regardons une photo à 30cm de notre œil.
ds=r.dϴ
dϴ = Π/180/60
r = 30 cm
>>>> ds = 0,0087 cm
Le plus petit détail que pourra discerner mon œil est légèrement inférieur au 1/10 de mm.
Donc une densité de pixels supérieure à 10 pixels/mm serait superflue car l’information supplémentaire ne peut être discriminée par l’œil.
Il suffit donc de 1,5 millions de pixels pour pouvoir tirer des photos de qualité tout à fait acceptable au format 10cm x 15 cm.
La course aux Mpixels entretenues par les fabricants d’appareil photo pour le grand public n’est utile … qu’à eux-mêmes !
J’exagère à peine. Pour ce cas, même en prenant une marge (5/100 mm), une densité ou résolution de 20 pixels/mm est suffisante.
Sauf, bien entendu, si vous voulez réaliser de la photo artistique ou des tirages au format A4, A3, voire plus …
Par homothétie, une affiche vue à 20m (ds = 5 mm) utilisant en projection la même photo de 1000x1500 pixels, 'pourrait' avoir les dimensions de 5m x 7,5m.
Certes pour éviter une pixellisation trop voyante il faut quand même s'en tenir à des dimensions un peu moindres ou utiliser une photo d'origine avec une meilleure résolution ...
Faire d’autres calculs pour puiser dans votre Livret (€) pour acquérir, par exemple, un Hasselblad à 60 Mpixels équipé d’un capteur 40.2 mm x 53.7 mm !!
Regardons une photo à 30cm de notre œil.
ds=r.dϴ
dϴ = Π/180/60
r = 30 cm
>>>> ds = 0,0087 cm
Le plus petit détail que pourra discerner mon œil est légèrement inférieur au 1/10 de mm.
Donc une densité de pixels supérieure à 10 pixels/mm serait superflue car l’information supplémentaire ne peut être discriminée par l’œil.
Il suffit donc de 1,5 millions de pixels pour pouvoir tirer des photos de qualité tout à fait acceptable au format 10cm x 15 cm.
La course aux Mpixels entretenues par les fabricants d’appareil photo pour le grand public n’est utile … qu’à eux-mêmes !
J’exagère à peine. Pour ce cas, même en prenant une marge (5/100 mm), une densité ou résolution de 20 pixels/mm est suffisante.
Sauf, bien entendu, si vous voulez réaliser de la photo artistique ou des tirages au format A4, A3, voire plus …
Par homothétie, une affiche vue à 20m (ds = 5 mm) utilisant en projection la même photo de 1000x1500 pixels, 'pourrait' avoir les dimensions de 5m x 7,5m.
Certes pour éviter une pixellisation trop voyante il faut quand même s'en tenir à des dimensions un peu moindres ou utiliser une photo d'origine avec une meilleure résolution ...
Faire d’autres calculs pour puiser dans votre Livret (€) pour acquérir, par exemple, un Hasselblad à 60 Mpixels équipé d’un capteur 40.2 mm x 53.7 mm !!
Coté écran, mon 17 pouces (diagonale de 43,2 cm, # 380mm x 214mm) peut afficher dans sa meilleure définition une matrice de 1600x900 pixels.
Soit donc une densité de # 4 pixels/mm.
Mon image 3648x2431 pixels est donc presque 3 fois trop résolue pour l'affichage (qui peut le + peut le -).
Soit donc une densité de # 4 pixels/mm.
Mon image 3648x2431 pixels est donc presque 3 fois trop résolue pour l'affichage (qui peut le + peut le -).
↑ Haut de page ↑
Le 09.04.2015
Les jeux de hasard
Pour ceux qui s’étonnent de ne jamais gagner au Loto, rappelons quelques principes élémentaires.
Plus concrètement, prenons l’exemple de l’Euro-millions.
Il se compose en fait de deux tirages :
- tirer 5 numéros dans la suite [1, 2, 3, … 49, 50]
- tirer 2 numéros dans la suite [1, 2, 3, …, 10, 11]
En mathématique c'est choisir une Combinaison (en l'occurrence deux).
Combien existe-t-il de combinaisons C de p éléments choisis dans un ensemble de n éléments distincts (notation Cnp) ?
La formule se démontre assez facilement : Cnp = n! /[p!(n-p)!]
Où l’opérateur n! désigne le produit des n nombres entiers inférieurs ou égaux à n, soit :
n! = 1x2x3x4x….(n-1)xn
Un exemple : 5! = 1x2x3x4x5 = 120
Les machines à calculer intègre de nos jours cette fonction.
Une combinaison C ne prend pas en compte l’ordre.
Prenons un exemple : les différentes associations possibles des 3 nombres 1,2,3 : [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2] et [3,2,1] ne compte que pour une combinaison (pour parler autrement, l’ordre de tirage n’intervient pas).
Pour revenir au cas qui nous intéresse, puisqu’il y a deux tirages distincts (l’un étant différencié avec des étoiles), on démontre facilement que le nombre total de combinaisons possibles (NC) est égal au produit du nombre de combinaisons de chacun des 2 tirages, Cnp et Kmq.
Cnp : n=50, p=5
Kmq : m=11, q=2
Pour une combinaison C, il existe Kmq combinaisons possibles
Pour une 2ième combinaison C, il existe encore Kmq combinaisons possibles
Pour une 3ième combinaison C, il existe encore et toujours Kmq combinaisons possibles
………
Ainsi de suite pour l’ensemble des combinaisons Cnp.
Et donc NC= Cnp x Kmq
Venons-en à l’Euro-millions :
C505 = 50!/[5!(50-5)!] = 50!/(5! x 45!) = (45!x46x47x48x49x50)/5!/45!
C505 = (46x47x48x49x50)/(1x2x3x4x5) = 254251200/120 = 2118760
De même :
K112 = 11!/[2!(11-2)!] = 11!/(2! x 9!) = (9!x10x11)/2!/9! = 10x11/2 = 55
Et donc
NC = 2118760 x 55 = 116 531 800 combinaisons possibles !
Probabilité < à 10-8
En imaginant le cas pire (why not car il y en aura un) où la combinaison que vous avez choisie ne sortirait qu’après toutes les autres (après 116 531 799 tirages) : comme il y a grosso-modo 100 tirages par an, vous devrez attendre … plus d’un million d’années !!!
Et encore, ici, on suppose que chaque combinaison sorte sans redondance …
Et d’un autre coté, vous pouvez gagner demain …
Bon, c'est surtout la FDJ ... et l'Etat (30% des mises) qui gagnent !
La chance, c’est le coté positif du hasard !
Pour ceux qui s’étonnent de ne jamais gagner au Loto, rappelons quelques principes élémentaires.
Plus concrètement, prenons l’exemple de l’Euro-millions.
Il se compose en fait de deux tirages :
- tirer 5 numéros dans la suite [1, 2, 3, … 49, 50]
- tirer 2 numéros dans la suite [1, 2, 3, …, 10, 11]
En mathématique c'est choisir une Combinaison (en l'occurrence deux).
Combien existe-t-il de combinaisons C de p éléments choisis dans un ensemble de n éléments distincts (notation Cnp) ?
La formule se démontre assez facilement : Cnp = n! /[p!(n-p)!]
Où l’opérateur n! désigne le produit des n nombres entiers inférieurs ou égaux à n, soit :
n! = 1x2x3x4x….(n-1)xn
Un exemple : 5! = 1x2x3x4x5 = 120
Les machines à calculer intègre de nos jours cette fonction.
Une combinaison C ne prend pas en compte l’ordre.
Prenons un exemple : les différentes associations possibles des 3 nombres 1,2,3 : [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2] et [3,2,1] ne compte que pour une combinaison (pour parler autrement, l’ordre de tirage n’intervient pas).
Pour revenir au cas qui nous intéresse, puisqu’il y a deux tirages distincts (l’un étant différencié avec des étoiles), on démontre facilement que le nombre total de combinaisons possibles (NC) est égal au produit du nombre de combinaisons de chacun des 2 tirages, Cnp et Kmq.
Cnp : n=50, p=5
Kmq : m=11, q=2
Pour une combinaison C, il existe Kmq combinaisons possibles
Pour une 2ième combinaison C, il existe encore Kmq combinaisons possibles
Pour une 3ième combinaison C, il existe encore et toujours Kmq combinaisons possibles
………
Ainsi de suite pour l’ensemble des combinaisons Cnp.
Et donc NC= Cnp x Kmq
Venons-en à l’Euro-millions :
C505 = 50!/[5!(50-5)!] = 50!/(5! x 45!) = (45!x46x47x48x49x50)/5!/45!
C505 = (46x47x48x49x50)/(1x2x3x4x5) = 254251200/120 = 2118760
De même :
K112 = 11!/[2!(11-2)!] = 11!/(2! x 9!) = (9!x10x11)/2!/9! = 10x11/2 = 55
Et donc
NC = 2118760 x 55 = 116 531 800 combinaisons possibles !
Probabilité < à 10-8
En imaginant le cas pire (why not car il y en aura un) où la combinaison que vous avez choisie ne sortirait qu’après toutes les autres (après 116 531 799 tirages) : comme il y a grosso-modo 100 tirages par an, vous devrez attendre … plus d’un million d’années !!!
Et encore, ici, on suppose que chaque combinaison sorte sans redondance …
Et d’un autre coté, vous pouvez gagner demain …
Bon, c'est surtout la FDJ ... et l'Etat (30% des mises) qui gagnent !
La chance, c’est le coté positif du hasard !

Crédit FdJ
↑ Haut de page ↑
Le 28.02.2015
Un sujet que j'ai découvert par hasard en lisant l'un des livres, passionnant, de J.C. Ameisen "Sur les épaules de Darwin : je t'offrirai des spectacles admirables ", le modèle proie/prédateur de Volterra-Lokta, du nom de ses découvreurs.
Je trouve extraordinaire qu'il ait été possible de quantifier la dynamique de systèmes tels que l'évolution de populations animales en compétition (biologie), l'étude du sommeil paradoxal et de l'état de veille (neurologie), voire le mouvement des dunes de sable du désert (physique).
Ces systèmes sont représentés par un couple d'équations différentielles non-linéaires du premier ordre. Je renvoie les mathématiciens et les puristes à la publication suivante émise dans le cadre d'une préparation à l'agrégation de mathématiques (!).
Examinons les équations qui régissent le système proies/prédateurs.
La variable t représente le temps. Soit x(t) et y(t) respectivement les populations de proies et de prédateurs fonction du temps.Les proies sont supposées disposer d'une source infinie de nourriture.
Je trouve extraordinaire qu'il ait été possible de quantifier la dynamique de systèmes tels que l'évolution de populations animales en compétition (biologie), l'étude du sommeil paradoxal et de l'état de veille (neurologie), voire le mouvement des dunes de sable du désert (physique).
Ces systèmes sont représentés par un couple d'équations différentielles non-linéaires du premier ordre. Je renvoie les mathématiciens et les puristes à la publication suivante émise dans le cadre d'une préparation à l'agrégation de mathématiques (!).
Examinons les équations qui régissent le système proies/prédateurs.
La variable t représente le temps. Soit x(t) et y(t) respectivement les populations de proies et de prédateurs fonction du temps.Les proies sont supposées disposer d'une source infinie de nourriture.
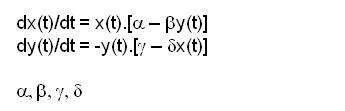
Alpha, Beta, Gamma et Delta sont des constantes illustrant les interactions entre les deux populations :
- alpha, taux de reproduction des proies (constant, indépendant du nombre de prédateurs)
- beta, taux de mortalité des proies dû aux prédateurs rencontrés
- gamma, taux de mortalité des prédateurs (constant, indépendant du nombre de proies)
- delta, taux de reproduction des prédateurs en fonction des proies rencontrées et mangées.
Pour une condition initiale x(t0)>0 et y(t0)>0 à t0 il existe une solution unique représentée ci-contre :
Interprétation :
Les prédateurs prospèrent lorsque les proies sont nombreuses, mais finissent par épuiser leurs ressources et leur population décline.
Lorsque la population de prédateurs a suffisamment diminué, les proies profitent du répit pour se reproduire et leur population augmente de nouveau.
Cette dynamique se poursuit en un cycle périodique en théorie infini.
Il exsite une nombreuse littérature sur le sujet.
Les prédateurs prospèrent lorsque les proies sont nombreuses, mais finissent par épuiser leurs ressources et leur population décline.
Lorsque la population de prédateurs a suffisamment diminué, les proies profitent du répit pour se reproduire et leur population augmente de nouveau.
Cette dynamique se poursuit en un cycle périodique en théorie infini.
Il exsite une nombreuse littérature sur le sujet.
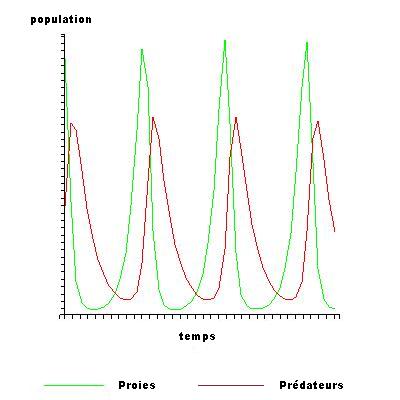
Ces sytèmes oscillatoires autour d'un état d'équilibre se retrouvent un peu partout dans la nature.
Plus tard, Turing, décrypteur des codes secrets nazis et inventeur de l'ordinateur (occasion de découvrir cet inventeur anglais, incarné par B. Cumberbatch dans le film Imitation Game), a aussi réalisé un modéle mathématique de réaction-diffusion qui sera vérifié expérimentalement en 1998 (génèse des formes).
Toujours ce couple activateur-inhibiteur.
Pour le reste, je renvoie au livre passionant de J.C. Ameisen qui nous prend par la main et nous emmène découvrir ces spectacles admirables.
Vous ne regarderez plus de la même façon le monde animal, végétal, minéral : fourmis, abeilles à miel, le monde qui nous entoure, le cosmos, les nombres, un flocon de neige ...
Je répète, passionnant.
Plus tard, Turing, décrypteur des codes secrets nazis et inventeur de l'ordinateur (occasion de découvrir cet inventeur anglais, incarné par B. Cumberbatch dans le film Imitation Game), a aussi réalisé un modéle mathématique de réaction-diffusion qui sera vérifié expérimentalement en 1998 (génèse des formes).
Toujours ce couple activateur-inhibiteur.
Pour le reste, je renvoie au livre passionant de J.C. Ameisen qui nous prend par la main et nous emmène découvrir ces spectacles admirables.
Vous ne regarderez plus de la même façon le monde animal, végétal, minéral : fourmis, abeilles à miel, le monde qui nous entoure, le cosmos, les nombres, un flocon de neige ...
Je répète, passionnant.

Apis mellifera
↑ Haut de page ↑
Le 22.12.2014


En 1970 les classes prépa faisaient toujours faire du "calcul numérique" avec ... cet objet (là, au-dessus).
Mais nous avons quand même éviter le boulier chinois !
Qui dit calcul, dit moyen de calcul.
Premier calculateur, un Wang, au début des années 70 (entrée manuelle des instructions machines !).
Puis le TEKTRONIX 4051, avec interpréteur (et non compilateur) qui a servi à programmer des centaines de lignes de BASIC.
Saut dans le futur, le PDP 11-60 de chez Digital sur lequel il fallait effacer les instructions au fur et à mesure de l'avancement des programmes pour gagner de la place mémoire ... Et son sucesseur le VAX.
Ces machines ont néammoins permis la mise en oeuvre de méthode de calcul jusque là inaccessible ou laborieuse. Exemple avec les différences finies (1D) dans le domaine du transfert de chaleur par discrétisation de l'équation de Fourier en milieu isotrope, propriétés fonctions de la Température avec différentes méthodes (schémas explicite, Cranck-Nicolson, implicite). Tout cela en FORTRAN ...
Mais nous avons quand même éviter le boulier chinois !
Qui dit calcul, dit moyen de calcul.
Premier calculateur, un Wang, au début des années 70 (entrée manuelle des instructions machines !).
Puis le TEKTRONIX 4051, avec interpréteur (et non compilateur) qui a servi à programmer des centaines de lignes de BASIC.
Saut dans le futur, le PDP 11-60 de chez Digital sur lequel il fallait effacer les instructions au fur et à mesure de l'avancement des programmes pour gagner de la place mémoire ... Et son sucesseur le VAX.
Ces machines ont néammoins permis la mise en oeuvre de méthode de calcul jusque là inaccessible ou laborieuse. Exemple avec les différences finies (1D) dans le domaine du transfert de chaleur par discrétisation de l'équation de Fourier en milieu isotrope, propriétés fonctions de la Température avec différentes méthodes (schémas explicite, Cranck-Nicolson, implicite). Tout cela en FORTRAN ...

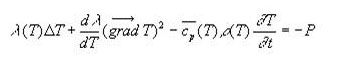
A l'époque, l'ONERA, pour ne point le nommer, était un organisme de recherche à la pointe de la technique.
Puis vint le réseau de Stations (SUN en particulier) sous Unix (à l'Aérospatiale, devenue EADS, et plus récemment AIRBUS Industrie)
Ensuite les CRAY à la fin des années 80/début 90.
Cray2 qui plafonnait joyeusement à l'époque à 2 gigaflops (2x109 opérations/s).
Toujours pour la modélisation des transferts d'énergie, dans des schémas avec couplages conductifs, radiatifs , voire convectifs, pour l'espace et la rentrée atmosphérique.
Approche numérique aussi par volumes finis (démarche plus proche de la physique).
Apparition du PC.
Un petit flirt avec EULER, équation de Navier-Stokes appliquée au fluide non visqueux.
Puis vint le réseau de Stations (SUN en particulier) sous Unix (à l'Aérospatiale, devenue EADS, et plus récemment AIRBUS Industrie)
Ensuite les CRAY à la fin des années 80/début 90.
Cray2 qui plafonnait joyeusement à l'époque à 2 gigaflops (2x109 opérations/s).
Toujours pour la modélisation des transferts d'énergie, dans des schémas avec couplages conductifs, radiatifs , voire convectifs, pour l'espace et la rentrée atmosphérique.
Approche numérique aussi par volumes finis (démarche plus proche de la physique).
Apparition du PC.
Un petit flirt avec EULER, équation de Navier-Stokes appliquée au fluide non visqueux.

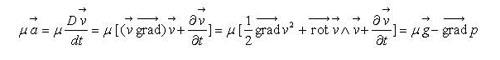
Ce fut aussi l'apparition, la généralisation et l'explosion des Eléments Finis qui avaient fait leurs preuves dans les calculs de structures (CEA et ses centrales)...
Oui, on atteint maintenant les 40 petaflops (2x1015opérations/s) avec un calculateur ... chinois (!).
Généralisation du calcul //.
Ceci dit, un PC, avec un core i5, développe quelque chose comme ~40 Gigaflops (~4x1010 opérations/s), soit 20 fois plus que le CRAY d'il y a 30 ans ....CQFD.
Au-delà de ces performances matériels, attrait pour tout ce qui touche à la Physique.
Peut être aussi une forme de fascination pour certaines équations.
Exemple, la fonction erreur, utilisée sur un projet :
Oui, on atteint maintenant les 40 petaflops (2x1015opérations/s) avec un calculateur ... chinois (!).
Généralisation du calcul //.
Ceci dit, un PC, avec un core i5, développe quelque chose comme ~40 Gigaflops (~4x1010 opérations/s), soit 20 fois plus que le CRAY d'il y a 30 ans ....CQFD.
Au-delà de ces performances matériels, attrait pour tout ce qui touche à la Physique.
Peut être aussi une forme de fascination pour certaines équations.
Exemple, la fonction erreur, utilisée sur un projet :
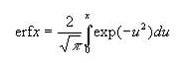

Alors que d'autres personnes semblent plus attirées par l'identité d'EULER
e i.p + 1 = 0, déclarée comme l'équation de l'Histoire il y a quelques années (?)(Télérama 3389-3390 24/12/14 p35).
Chacun ses défauts.
Après ces années plongées dans les nombres et les modèles, passage à des activités Programmatiques, en laissant la place aux esprits plus affutés pour résoudre des équations aux dérivées partielles !
Mais les calculs, effectivement, encore quelques souvenirs....!
Oublier que ʃ u.dv = u.v – ʃ v.du serait le signe avant-coureur d'une certaine maladie incurable ...
Aujourd'hui le bon vieux Formulaire Technique (GIECK) reste une référence pour envisager de nombreux petits calculs de la vie courante, que ce soit en thermique, en mécanique et autres domaines ...
e i.p + 1 = 0, déclarée comme l'équation de l'Histoire il y a quelques années (?)(Télérama 3389-3390 24/12/14 p35).
Chacun ses défauts.
Après ces années plongées dans les nombres et les modèles, passage à des activités Programmatiques, en laissant la place aux esprits plus affutés pour résoudre des équations aux dérivées partielles !
Mais les calculs, effectivement, encore quelques souvenirs....!
Oublier que ʃ u.dv = u.v – ʃ v.du serait le signe avant-coureur d'une certaine maladie incurable ...
Aujourd'hui le bon vieux Formulaire Technique (GIECK) reste une référence pour envisager de nombreux petits calculs de la vie courante, que ce soit en thermique, en mécanique et autres domaines ...
En cas de cataclysme planétaire, qui, parmi ces milliards d'utilisateurs d'ordinateurs, de tablette, d'iPad, saurait reconstruire un processeur ....?
↑ Haut de page ↑
SITE D'INFORMATIONS GENERALES
Plus de 180 rubriques réparties dans 11 thèmes
Désolé, pas de réseaux sociaux ici, qui n'ont de social que le nom ...
Droits réservés sur le contenu du site
Création et maintenance D. ORY © Février 2014 V2.1



