Le 22.12.2014 Notions d'Energie >>

Table d'orientation du site>>

SCIENCES & TECHNIQUES
Date heure
Informations générales : Energie, Structures, Espace, Climat, réalisations, calculs, ...
ENERGIE
Le 10.01.2015 Ouvrages de référence >>
Le 13.03.2015 L'effusivité >>
Le 19.04.2015 Notions fondamentales >>
Le 20.04.2015 L'énergie solaire >>
Le 22.04.2016 PTE ou PTI ? >>
Le 09.05.2016 Simulations PTE/PTI >>
Le 01.07.2016 Simulations : pour aller plus loin >>
Le 17.01.2017 Froid ressenti >>
Le 14.03.2017 Nucléaire >>
Le 29.05.2019 Centrale solaire >>
Le 16.11.2022 Initiative 110 km/h >>
Le 24.11.2022 Combustibles fossiles >>
Le 12.12.2022 Eoliennes >>
Le 12.12.2022
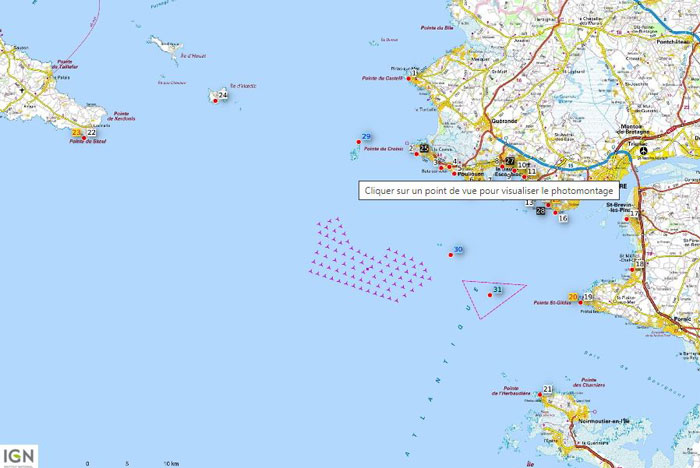
Eoliennes
Le parc éolien de St Nazaire est en cours de finalisation, la mise en service est prévue pour la fin de l'année 2022.
80 éoliennes situées entre 12km et 20km de la cote.
480MW de puissance nominale.
Le photomontage des hauteurs visibles de différentes plages donne une bonne idée de la réalité.
Indépendamment du débat pour ou contre, je signale un article paru dans la revue SAUVETAGE de la SNSM du 4ième trimestre 2022 qui s'intéresse aux impacts sécurité à prendre en compte pour les interventions de sauvetage dans un champ d'éoliennes.
L'article est ici.
80 éoliennes situées entre 12km et 20km de la cote.
480MW de puissance nominale.
Le photomontage des hauteurs visibles de différentes plages donne une bonne idée de la réalité.
Indépendamment du débat pour ou contre, je signale un article paru dans la revue SAUVETAGE de la SNSM du 4ième trimestre 2022 qui s'intéresse aux impacts sécurité à prendre en compte pour les interventions de sauvetage dans un champ d'éoliennes.
L'article est ici.
↑ Haut de page ↑
Le 24.11.2022
Combustibles fossiles
Quelques rappels.
Tous les combustibles fossiles émettent du CO2 en s'oxydant suivant les relations ci-contre (combustion parfaite).
Tous les combustibles fossiles émettent du CO2 en s'oxydant suivant les relations ci-contre (combustion parfaite).
Essence : C7H16 + 11 02 >>>> 7 CO2 + 8 H20
Gazole : 4 C7.25H13 + 36 O2 >>>> 30 CO2 + 16 H2O
Charbon : C + O2 >>>> CO2
Méthane : CH4 + 2 O2 >>>> CO2 + 2 H2O
butane 2 C4H10 + 13O2 >>>> 8 CO2 + 10 H20
SOURCE
Gazole : 4 C7.25H13 + 36 O2 >>>> 30 CO2 + 16 H2O
Charbon : C + O2 >>>> CO2
Méthane : CH4 + 2 O2 >>>> CO2 + 2 H2O
butane 2 C4H10 + 13O2 >>>> 8 CO2 + 10 H20
SOURCE
Donc plus ces combustibles sont utilisés, plus la part de CO2 dans l'atmosphère augmente.
Or il est prouvé (voir rubriques [1] et [2] dans le thème Climat) que l'accumulation des GES a un effet sur la température moyenne à la surface de la terre qui a commencé à augmenter à la fin du XIXième siècle.
Même si ces GES, en particulier le CO2, sont naturellement présents et entrent dans le fonctionnement de l'équilibre thermique à la surface de la terre, cet équilibre peut être rompu...
Que se passe-til ?
Le système thermodynamique cherche un nouvel équilibre radiatif suivant le schéma ci-contre.
Or il est prouvé (voir rubriques [1] et [2] dans le thème Climat) que l'accumulation des GES a un effet sur la température moyenne à la surface de la terre qui a commencé à augmenter à la fin du XIXième siècle.
Même si ces GES, en particulier le CO2, sont naturellement présents et entrent dans le fonctionnement de l'équilibre thermique à la surface de la terre, cet équilibre peut être rompu...
Que se passe-til ?
Le système thermodynamique cherche un nouvel équilibre radiatif suivant le schéma ci-contre.
.jpg)
Toute chose égale par ailleurs (voir bilan complet) :
- la surface de la terre est bien à l'équilibre : flux absorbé (168+324 +Δ) = flux émis (78+24+390+Δ) W/m2
- l'atmosphère est à l'équilibre : flux absorbé=flux émis (67+78+24+350+Δ) = (324+195+Δ) W/m2
- la surface de la terre est bien à l'équilibre : flux absorbé (168+324 +Δ) = flux émis (78+24+390+Δ) W/m2
- l'atmosphère est à l'équilibre : flux absorbé=flux émis (67+78+24+350+Δ) = (324+195+Δ) W/m2
Approche très théorique mais pédagogique. Les 1,5°C de réchauffement moyen constatés à ce jour par rapport aux 15°C moyens antérieurs (390W/m2 de flux IR) conduisent à 398W/m2, soit Δ=8W/m2 (rappel loi de Planck simplifiée Φ = σ . T4).
Ce n'est pas grand chose mais c'est beaucoup de conséquences dans la manière dont s'opère ce ré-équilibrage....
Ce n'est pas grand chose mais c'est beaucoup de conséquences dans la manière dont s'opère ce ré-équilibrage....
Revenons à nos combustibles fossiles.
Puisqu'il est question parfois de barils, parfois de tonnes, et les différents gisements de pétrole n'ayant pas tous les mêmes propriétés, la correspondance moyenne admise est 7,33 barils pour une tonne.
(1 baril ~ 159 l)
Puisqu'il est question parfois de barils, parfois de tonnes, et les différents gisements de pétrole n'ayant pas tous les mêmes propriétés, la correspondance moyenne admise est 7,33 barils pour une tonne.
(1 baril ~ 159 l)
En France nous consommons encore #71 millions de tonnes de pétrole et #37 millions de T.E.P. en gaz par an.
Sur l'ensemble de la planète c'est de l'ordre de #4 milliards de tonnes de pétrole qui ont été consommées en 2021 !!
Sur l'ensemble de la planète c'est de l'ordre de #4 milliards de tonnes de pétrole qui ont été consommées en 2021 !!
De même la production, et donc la consommation, de gaz naturel s'est élevée à #3900 milliards de m3 en 2020 !!
Or les réserves connues et prouvées (principaux fournisseurs : Russie, Iran, Qatar, Tukménistan, USA : 76% des réserves, 50% pour les 3 premiers) se chiffrent à 188,1 milliers de milliards de m3 à la fin de l’année 2020 !
Or les réserves connues et prouvées (principaux fournisseurs : Russie, Iran, Qatar, Tukménistan, USA : 76% des réserves, 50% pour les 3 premiers) se chiffrent à 188,1 milliers de milliards de m3 à la fin de l’année 2020 !
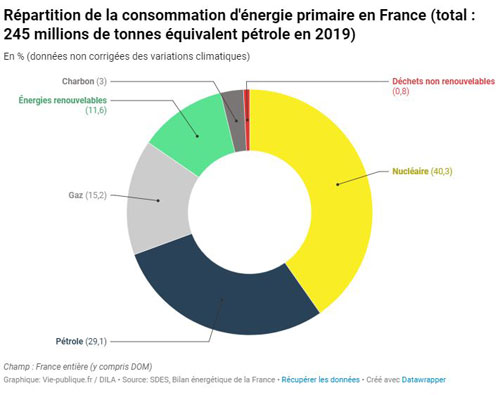
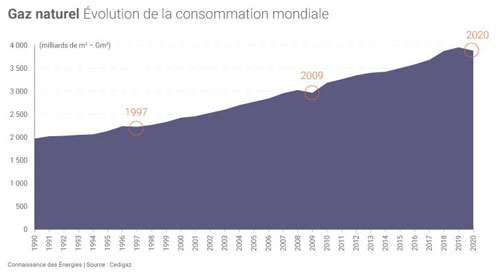
Au rythme actuel il resterait 50 années de production !
Credit www.vie-publique.fr
Au cours actuels de nombreux pays producteurs (pétrole, gaz) ont des mines d'or sous leurs pieds.
Je doute que certains de ces pays se privent rapidement de cette richesse au nom de la protection du climat ... Ainsi le gisement de gaz sous le Golfe Persique, exploité par le Qatar et l'Iran. Le Qatar estime qu'il pourra l'exploiter jusqu'à la fin du siècle !
De plus l’exploitation de gisements dans des zones profondes ou ultra-profondes est en plein développement malgré les défis techniques : l’épuisement de ces réserves n’est certainement pas encore pour demain ...
Espérer la transition énergétique en pariant sur un tarissement des réserves est donc vain. La sortie des énergies fossiles (pétrole, gaz, etc) ne se fera qu’en fonction de notre volonté et celle des gouvernements prêts à imposer un réel changement.
C'est toutefois ce que la guerre en Ukraine a enclenché à l'échelle de l'Europe.
Je doute que certains de ces pays se privent rapidement de cette richesse au nom de la protection du climat ... Ainsi le gisement de gaz sous le Golfe Persique, exploité par le Qatar et l'Iran. Le Qatar estime qu'il pourra l'exploiter jusqu'à la fin du siècle !
De plus l’exploitation de gisements dans des zones profondes ou ultra-profondes est en plein développement malgré les défis techniques : l’épuisement de ces réserves n’est certainement pas encore pour demain ...
Espérer la transition énergétique en pariant sur un tarissement des réserves est donc vain. La sortie des énergies fossiles (pétrole, gaz, etc) ne se fera qu’en fonction de notre volonté et celle des gouvernements prêts à imposer un réel changement.
C'est toutefois ce que la guerre en Ukraine a enclenché à l'échelle de l'Europe.
↑ Haut de page ↑
Le 16.11.2022
Initiative 110 km/h
Une règle que je m'applique depuis des mois quand je suis sur l'autoroute et pour laquelle quelques personnalités (C. Dion, JM Jancovici, etc ...) ont lancé un appel dans le JDD : rouler à 110 km/h sur autoroute.
Pourquoi ?
Petite initiative parmi des milliers d'autres qui repose sur le volontariat de chaque individu et qui a un double effet immédiat, bénéfique à deux titres : économie d'énergie et baisse d'émission de GES (CO2 en particulier ).
Pas de chance, Mme Borne a rénoncé, sous prétexte 'qu'on ne peut fonctionner à coups d'interdictions'. Ite missa est !
Combien de temps pour parcourir 130km à 110km/h ? 1,18h soit 11mn de plus qu'à 130km/h
Pourquoi ?
Petite initiative parmi des milliers d'autres qui repose sur le volontariat de chaque individu et qui a un double effet immédiat, bénéfique à deux titres : économie d'énergie et baisse d'émission de GES (CO2 en particulier ).
Pas de chance, Mme Borne a rénoncé, sous prétexte 'qu'on ne peut fonctionner à coups d'interdictions'. Ite missa est !
Combien de temps pour parcourir 130km à 110km/h ? 1,18h soit 11mn de plus qu'à 130km/h
Et pourtant ...
Une fois le démarrage réalisé et les forces de frottement vaincues un véhicule automobile doit lutter contre les forces aérodynamiques F pour maintenir sa vitesse.
F s'exprime par : F = 1/2.ρ.S.V2. Cx
C'est le moteur du véhicule qui créée la force motrice pour contrer cette résistance et pour atteindre et maintenir cette vitesse.
De 110km/h (F1) à 130km/h (F2) le rapport des forces aéro est :
F2/F1# [36/30]2
soit F2 # 1,44.F1 ce qui n'est pas négligeable.
Une fois le démarrage réalisé et les forces de frottement vaincues un véhicule automobile doit lutter contre les forces aérodynamiques F pour maintenir sa vitesse.
F s'exprime par : F = 1/2.ρ.S.V2. Cx
- ρ : masse volumique de l'air kg/m3
- S : sestion droite du véhicule m2
- V : vitesse m/s
- Cx : coefficient de trainée en rapport avec l'aérodynamisme du véhicule
C'est le moteur du véhicule qui créée la force motrice pour contrer cette résistance et pour atteindre et maintenir cette vitesse.
De 110km/h (F1) à 130km/h (F2) le rapport des forces aéro est :
F2/F1# [36/30]2
soit F2 # 1,44.F1 ce qui n'est pas négligeable.
Credit https://www.astuces-pratiques.fr/
Quid de la consommation derrière ce constat ?
Je ne referai pas les calculs pour la démonstration.
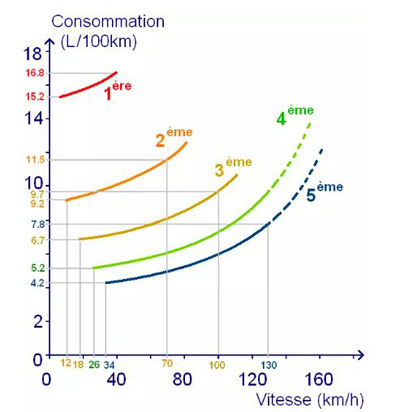
Je me contente de reprendre des courbes types vitesse/consommation.
La consommation est directement liée au régime moteur, à vitesse donnée, plus le régime est bas (nombre de tour/mn), plus faible est la consommation, donc rouler en 5ième ou 6ième vitesse dès que possible (régime stabilisé).
C'est ce que montre cette abaque, plus ou moins applicable en moyenne suivant le type de carburant et de moteur à tous les constructeurs.
Donc pour faire nos 130km à 110km/h gain de 1,69l soit 3,38€ pour une perte de temps de 11mn par rapport à 130km/h ... CQFD
26€ économisés tous les 1000km pour un temps supplémentaires de 1h24mn. Il faut choisir ...
Je ne referai pas les calculs pour la démonstration.
Je me contente de reprendre des courbes types vitesse/consommation.
La consommation est directement liée au régime moteur, à vitesse donnée, plus le régime est bas (nombre de tour/mn), plus faible est la consommation, donc rouler en 5ième ou 6ième vitesse dès que possible (régime stabilisé).
C'est ce que montre cette abaque, plus ou moins applicable en moyenne suivant le type de carburant et de moteur à tous les constructeurs.
- 7,8l/100km à 130km/h
- 6,5l/100km à 110km/h
Donc pour faire nos 130km à 110km/h gain de 1,69l soit 3,38€ pour une perte de temps de 11mn par rapport à 130km/h ... CQFD
26€ économisés tous les 1000km pour un temps supplémentaires de 1h24mn. Il faut choisir ...
J'ai été surpris de lire dans Science et Vie (novembre 2022) que l'humanité avait utilisé environ 270 milliards de tonnes de pétrole depuis le début du XXième siècle mais que les réserves déjà découvertes et exploitables représentaient 280 milliards de tonnes et que les réserves non découvertes et économiquement rentables représenteraient encore 80 milliards de tonnes ! [*]
De quoi durablement impacter le réchauffement climatique !
J'en viens à douter qu'on se débarasse vite et bien du roi pétrole ...
L'humanité consommant en moyenne 4 milliards de tonnes par an il resterait jusqu'à 90 ans de consommation au rythme actuel ....!
Or les projections montrent qu'il ne faudrait pas consommer plus de 150 milliards de tonnes (émissions de Cxx), ce qui conduit en 2059, pour limiter l'élévation de température moyennne de la planète à 1,5°C.
Aujourd'hui encore le pétrole reste le principal carburant de l'économie mondiale.
Avec un baril de Brent qui oscille entre 80$ et 100$ les pétrodollars tombent encore dans les poches des pays producteurs et des compagnies pétrolières.
C'est tout le dilemme pour les pays en voie de développement qui réclament le droit à consommer cette énergie, n'étant pas à l'origine du réchauffement climatique.
Notons qu'il y avait encore un nombre record de lobbyistes (charbon, gaz, pétrole) à la COP27 ....
[*] j'ai retenu les fourchettes hautes
De quoi durablement impacter le réchauffement climatique !
J'en viens à douter qu'on se débarasse vite et bien du roi pétrole ...
L'humanité consommant en moyenne 4 milliards de tonnes par an il resterait jusqu'à 90 ans de consommation au rythme actuel ....!
Or les projections montrent qu'il ne faudrait pas consommer plus de 150 milliards de tonnes (émissions de Cxx), ce qui conduit en 2059, pour limiter l'élévation de température moyennne de la planète à 1,5°C.
Aujourd'hui encore le pétrole reste le principal carburant de l'économie mondiale.
Avec un baril de Brent qui oscille entre 80$ et 100$ les pétrodollars tombent encore dans les poches des pays producteurs et des compagnies pétrolières.
C'est tout le dilemme pour les pays en voie de développement qui réclament le droit à consommer cette énergie, n'étant pas à l'origine du réchauffement climatique.
Notons qu'il y avait encore un nombre record de lobbyistes (charbon, gaz, pétrole) à la COP27 ....
[*] j'ai retenu les fourchettes hautes
↑ Haut de page ↑
Le 29.05.2019
Centrale solaire
J'en avais parlé un peu là pour le four solaire d'Odeillo.
Il se trouve que par hasard lors d'un voyage en Andalousie j'ai pu apercevoir, subrepticement par la fenêtre d'un bus entre Séville et Cordoue, une centrale solaire en fonctionnement.
Il se trouve que par hasard lors d'un voyage en Andalousie j'ai pu apercevoir, subrepticement par la fenêtre d'un bus entre Séville et Cordoue, une centrale solaire en fonctionnement.

Renseignements pris, il s'agit du projet GEMASOLAR dont le site comporte 2 tours, la dernière (PS20) ayant été mise en service en 2009. Plus de 2600 héliostats concentrent le rayonnement solaire en haut de la tour pour fournir une puissance électrique de 17MW.
Vous en saurez plus en consultant ce site.
Originalité : elle peut continuer à fournir de l'énergie pendant une quinzaine d'heures sans soleil grâce au stockage des sels fondus.
La conversion d'énergie solaire en électricité se fait suivant le principe :
Il ne s'agit plus comme à Odeillo d'un centre de recherche mais d'une application industrielle.
Vous en saurez plus en consultant ce site.
Originalité : elle peut continuer à fournir de l'énergie pendant une quinzaine d'heures sans soleil grâce au stockage des sels fondus.
La conversion d'énergie solaire en électricité se fait suivant le principe :
- > sels fondus à 565°C en haut de la tour
- > échange d'énergie via un générateur de vapeur
- > turbine actionnée par la vapeur HP
- > Production d'électricité injectée dans le réseau
Il ne s'agit plus comme à Odeillo d'un centre de recherche mais d'une application industrielle.
Grâce à ses conditions d'ensoleillement très favorables cette région d'Espagne est particulièrement adaptée à cette technologie, tout comme d'ailleurs le photovoltaïque à grande échelle.
Je suis certain que les travaux menés dans les années 1970 en France ont participé au développement de ces projets.
La France qui a d'ailleurs continué dans cette voie : non loin d'Odeillo, Thémis est la centrale solaire thermodynamique qui a produit de l'électricité pour le réseau Électricité de France (EDF) de 1983 à 1986.
Située en Cerdagne à Targassonne dans les Pyrénées-Orientales, elle a été réhabilitée depuis 2004, pour devenir Thémis Solaire Innovation, centre de recherche et de développement consacré à l'énergie solaire (thermodynamique et photovoltaïque).
Dans les projets en cours la centrale eLLO est une centrale solaire thermodynamique qui va produire de l'électricité pour le réseau Électricité de France (EDF). Elle est située à Llo, commune des Pyrénées-Orientales, et a été conçue par la filiale SUNCNIM de la société CNIM.
Ici le soleil éclaire un champ de récepteurs plan concentrant l'énergie par un système de lentille de Fresnel sur un tube où circule de l'eau.
La conversion en électricité se fait suivant le même principe (Vapeur + turbine). La puissance électrique attendue est de 9MW.
Je suis certain que les travaux menés dans les années 1970 en France ont participé au développement de ces projets.
La France qui a d'ailleurs continué dans cette voie : non loin d'Odeillo, Thémis est la centrale solaire thermodynamique qui a produit de l'électricité pour le réseau Électricité de France (EDF) de 1983 à 1986.
Située en Cerdagne à Targassonne dans les Pyrénées-Orientales, elle a été réhabilitée depuis 2004, pour devenir Thémis Solaire Innovation, centre de recherche et de développement consacré à l'énergie solaire (thermodynamique et photovoltaïque).
Dans les projets en cours la centrale eLLO est une centrale solaire thermodynamique qui va produire de l'électricité pour le réseau Électricité de France (EDF). Elle est située à Llo, commune des Pyrénées-Orientales, et a été conçue par la filiale SUNCNIM de la société CNIM.
Ici le soleil éclaire un champ de récepteurs plan concentrant l'énergie par un système de lentille de Fresnel sur un tube où circule de l'eau.
La conversion en électricité se fait suivant le même principe (Vapeur + turbine). La puissance électrique attendue est de 9MW.
J'ai pu apercevoir (à droite sur la photo) une dernière fois le site espagnol depuis l'avion qui m'emmenait vers Paris ...

↑ Haut de page ↑
Le 14.03.2017
Nucléaire
Il y a trois jours le Japon commémorait le sixième anniversaire de la catastrophe nucléaire de Fukushima le 11 mars 2011.
L'article de Sud-Ouest, parmi d'autres, résume bien la situation.
L'article de Sud-Ouest, parmi d'autres, résume bien la situation.
Fait qui parait incroyable après cette catastrophe, le Japon a re-ouvert l'une de ses centrales, précisément le complexe de Sendai, sur l’île de Kyushu (voir carte), malgré l'opposition de la majorité de la population.
L'écrivain japonais Akira Mizubayashi, vivant en France, parle de déni de la part du gouvernement, voire de retour en arrière favorisé par la culture japonaise qui manifeste une indifférence collective, une propension à la soumission.
Les voix de quelques-uns ne suffisent pas à donner d'essor à une opinion publique critique ...
Pire encore il semble qu'il y ait vexations, jalousie (!) et harcèlement envers les personnes déplacées, qui, les pauvres, n'y sont pour rien.
L'écrivain japonais Akira Mizubayashi, vivant en France, parle de déni de la part du gouvernement, voire de retour en arrière favorisé par la culture japonaise qui manifeste une indifférence collective, une propension à la soumission.
Les voix de quelques-uns ne suffisent pas à donner d'essor à une opinion publique critique ...
Pire encore il semble qu'il y ait vexations, jalousie (!) et harcèlement envers les personnes déplacées, qui, les pauvres, n'y sont pour rien.
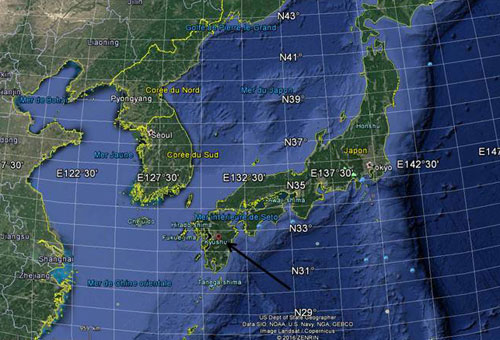
Credit Google
Pourtant la géologie du sous-sol, particulièrement instable, est bien connue dans cette région : c'est le point de rencontre des plaques Eurasiatique, Nord-Américaine, Pacifique et Philippines, avec un grand nombres de volcans actifs et de tremblements de terres, quasi continuels, voir cette carte qui comptabilise les secousses avec leur intensité, depuis des années ...
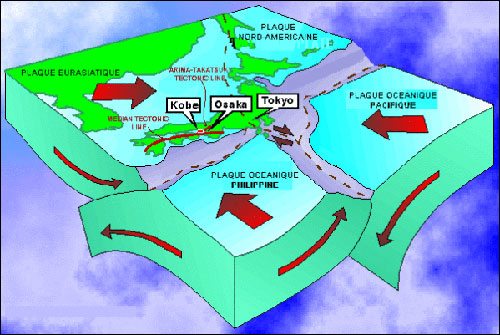
earth-of-fire.over-blog.com
On parle de la mondialisation uniquement sous l'aspect commercial, mais il faudra bien un jour en parler plus sérieusement d'un point de vue politique (je fais abstraction de l'ONU, organisme qui semble aujourd'hui un peu impuissant), une mondialisation des citoyens ... Utopie ?
Certes, nous en sommes loin, je dirai même, nous faisons marche arrière avec tous ces prophètes nationalistes qui prèchent la haine et la construction de murs un peu partout dans le monde.
En effet est-il raisonnable que le communauté internationnale se taise : laisser construire des centrales nucléaires dans une zone sismique fortement active ? Nous retombons dans la problématique précédente : nation = décision souveraine, sans contre-pouvoir international.
Certes, dira-t-on, le Japon a aussi besoin de source d'énergie pour vivre et se développer, mais ceci n'est pas remis en cause.
Toute cette problématique devrait se négocier dans une instance supra-nationale ....
Le monde, du moins la majorité des peuples, n'a pas encore pris conscience que la Terre est notre vaisseau spatial commun duquel nous ne pourrons nous détacher ... pas avant quelques siècles ! (si la terre est encore vivable)
Pour pousser le raisonnement encore plus loin, les ressources naturelles de toutes sortes que nous procure la terre appartiennent à tous les humains et devraient être partagées équitablement.
J'ai bien conscience là que nous en sommes très très loin !
Certes, nous en sommes loin, je dirai même, nous faisons marche arrière avec tous ces prophètes nationalistes qui prèchent la haine et la construction de murs un peu partout dans le monde.
En effet est-il raisonnable que le communauté internationnale se taise : laisser construire des centrales nucléaires dans une zone sismique fortement active ? Nous retombons dans la problématique précédente : nation = décision souveraine, sans contre-pouvoir international.
Certes, dira-t-on, le Japon a aussi besoin de source d'énergie pour vivre et se développer, mais ceci n'est pas remis en cause.
Toute cette problématique devrait se négocier dans une instance supra-nationale ....
Le monde, du moins la majorité des peuples, n'a pas encore pris conscience que la Terre est notre vaisseau spatial commun duquel nous ne pourrons nous détacher ... pas avant quelques siècles ! (si la terre est encore vivable)
Pour pousser le raisonnement encore plus loin, les ressources naturelles de toutes sortes que nous procure la terre appartiennent à tous les humains et devraient être partagées équitablement.
J'ai bien conscience là que nous en sommes très très loin !
Revenons à l'énergie nucléaire : le débat est loin d'être clos en France entre partisans et opposants ...
Des analyses contradictoires sont régulièrement menées pour souligner les avantages et les inconvénients de cette source d'énergie, les seconds étant, me semble-t-il, objectivement majoritaires (je laisse le lecteur parcourir les nombreux sites qui abordent ce sujet pour se faire un avis)
La France a voté une loi pour la transition énergétique en 2015.
L'Artcle 100, explicite, est ainsi rédigé :
'... La politique énergétique préserve la santé humaine et l'environnement, ... en particulier en réduisant l'exposition des citoyens à la pollution de l'air et en garantissant la sûreté nucléaire ...'
' ... réduire la part du nucléaire dans la production d'électricité à 50 % à l'horizon 2025 ...',
part qui est aujourd'hui de 76%, record du monde !
Des analyses contradictoires sont régulièrement menées pour souligner les avantages et les inconvénients de cette source d'énergie, les seconds étant, me semble-t-il, objectivement majoritaires (je laisse le lecteur parcourir les nombreux sites qui abordent ce sujet pour se faire un avis)
La France a voté une loi pour la transition énergétique en 2015.
L'Artcle 100, explicite, est ainsi rédigé :
'... La politique énergétique préserve la santé humaine et l'environnement, ... en particulier en réduisant l'exposition des citoyens à la pollution de l'air et en garantissant la sûreté nucléaire ...'
' ... réduire la part du nucléaire dans la production d'électricité à 50 % à l'horizon 2025 ...',
part qui est aujourd'hui de 76%, record du monde !
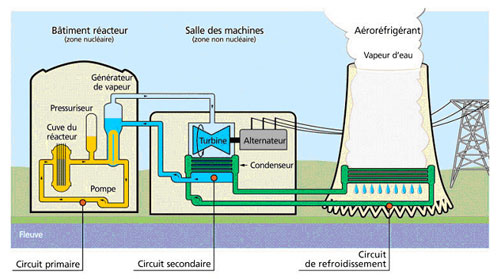
Certes il n'y a jamais eu de catastrophe dans une centrale française mais, malgré les progrès de l'analyse de risques et de sureté, le risque zéro n'existe pas ! (les artisans de Tchernobyl et de Fukushima étaient persuadés du contraire ...).
Et la promotion de la culture de sûreté, comme la préconisent certains, ne suffira pas.
Rappelons quelques chiffres sur les déchets radio-actifs : le radium est un déchet à vie moyenne. En effet, sa demi-vie (voir Conférence Climat planche 13), n'est que de1600 ans comparé à l'uranium, déchet radioactif à vie longue dont la demi-vie est d'environ 4 milliard et demi d'années. Il existe des déchets radioactifs à vie courte dont la demi-vie tourne autour 30 ans tel que le césium et le trontium.
Quel bazarre pour nos descendants.
Plus encore que la sureté, le vrai problème concerne donc les déchets et les centrales elles-même, deux élements factuels.
Ce "combat" semble peu nous (je me mets dedans) concerner : du moment que chacun allume sa lumière, son poste de télé et charge son portable ....
Vision individualiste du siècle passé et présent.
Un peu comme pour les hommes politiques : il faut un scandale pour que des mesures de transparences soient prises.
Toujours un temps de retard.
Sauf qu'ici il sera vraiment trop tard !
Et la promotion de la culture de sûreté, comme la préconisent certains, ne suffira pas.
Rappelons quelques chiffres sur les déchets radio-actifs : le radium est un déchet à vie moyenne. En effet, sa demi-vie (voir Conférence Climat planche 13), n'est que de1600 ans comparé à l'uranium, déchet radioactif à vie longue dont la demi-vie est d'environ 4 milliard et demi d'années. Il existe des déchets radioactifs à vie courte dont la demi-vie tourne autour 30 ans tel que le césium et le trontium.
Quel bazarre pour nos descendants.
Plus encore que la sureté, le vrai problème concerne donc les déchets et les centrales elles-même, deux élements factuels.
Ce "combat" semble peu nous (je me mets dedans) concerner : du moment que chacun allume sa lumière, son poste de télé et charge son portable ....
Vision individualiste du siècle passé et présent.
Un peu comme pour les hommes politiques : il faut un scandale pour que des mesures de transparences soient prises.
Toujours un temps de retard.
Sauf qu'ici il sera vraiment trop tard !
Une petites mise au point concernant l'Allemagne : contrairement à qu'on peut entendre ici où là, le charbon n'y a pas remplacé le nucléaire.
Certes il reste dans le pays tout de même une centaine de centrales à charbon en activité dont on connait les impacts écologiques et notamment la pollution de l’air provoquée par les émissions de particules fines.
Mais la baisse des émissions de GES, entamée depuis 1990, s'est simplement ralentie depuis 2011 comme le montre l'un des schémas de cet article.
Certes il reste dans le pays tout de même une centaine de centrales à charbon en activité dont on connait les impacts écologiques et notamment la pollution de l’air provoquée par les émissions de particules fines.
Mais la baisse des émissions de GES, entamée depuis 1990, s'est simplement ralentie depuis 2011 comme le montre l'un des schémas de cet article.
↑ Haut de page ↑
Le 17.01.2017
Froid ressenti

Credit Twitter La Pierre St Martin
La "vague de froid" fait parler d'elle cette semaine, comme si cet évènement revêtait un caractère exceptionnel.
Certes il n'avait pas, ou quasiment pas, gelé dans le quart sud-ouest de la France depuis quelques années. Les premiers à en faire les frais étaient ... les stations de sport d'hiver, en particulier dans les Pyrénées.
Ceci est à mettre au compte de la variabilité naturelle du climat, toujours là et nullement en contradiction avec l'évolution du climat au niveau de la planète ...
J'ai lu sur slate cet article qui parle du froid, de la baisse des températures et du ressenti par le corps humain. Et je vois que depuis que j'ai commencé cette rubrique le Monde et Sud-Ouest ont repris le sujet ...
Bref, c'est un sujet qui occupe les pages de nos gazettes.
Qu'elle est donc cette relation entre température mesurée et température perçue par le corps ?
Comment est-elle déterminée ?
Certes il n'avait pas, ou quasiment pas, gelé dans le quart sud-ouest de la France depuis quelques années. Les premiers à en faire les frais étaient ... les stations de sport d'hiver, en particulier dans les Pyrénées.
Ceci est à mettre au compte de la variabilité naturelle du climat, toujours là et nullement en contradiction avec l'évolution du climat au niveau de la planète ...
J'ai lu sur slate cet article qui parle du froid, de la baisse des températures et du ressenti par le corps humain. Et je vois que depuis que j'ai commencé cette rubrique le Monde et Sud-Ouest ont repris le sujet ...
Bref, c'est un sujet qui occupe les pages de nos gazettes.
Qu'elle est donc cette relation entre température mesurée et température perçue par le corps ?
Comment est-elle déterminée ?
"La couche d'air chaud, fabriquée par l'organisme, est dégagée par le vent, et le corps doit puiser beaucoup plus d’énergie pour refabriquer cette couche" nous dit le prévisionniste de Météo-France.
J'exprimerai ce phénomène autrement, en disant que tout ceci résulte d'un subtil équilibre thermique, rompu à un instant donné par l'effet du vent.
J'ai tracé ci-dessous la table fournie dans l'article. C'est en quelque sorte un abaque correcteur.
Comment interpréter ces courbes ?
La sensation physiologique avec les conditions (Text=-10°C [courbe verte/triangle], V=30km/h) est la même que celle ressentie avec les conditions (Text=-20°C [courbe bleue étoile], V nul).
Autre cas : la sensation physiologique avec les conditions (Text=-35°C [courbe mauve], V=23km/h) est la même que celle ressentie avec les conditions (Text=-50°C [courbe bleue carré], V nul).
Ce qui parait cohérent en soi ...
J'exprimerai ce phénomène autrement, en disant que tout ceci résulte d'un subtil équilibre thermique, rompu à un instant donné par l'effet du vent.
J'ai tracé ci-dessous la table fournie dans l'article. C'est en quelque sorte un abaque correcteur.
Comment interpréter ces courbes ?
La sensation physiologique avec les conditions (Text=-10°C [courbe verte/triangle], V=30km/h) est la même que celle ressentie avec les conditions (Text=-20°C [courbe bleue étoile], V nul).
Autre cas : la sensation physiologique avec les conditions (Text=-35°C [courbe mauve], V=23km/h) est la même que celle ressentie avec les conditions (Text=-50°C [courbe bleue carré], V nul).
Ce qui parait cohérent en soi ...
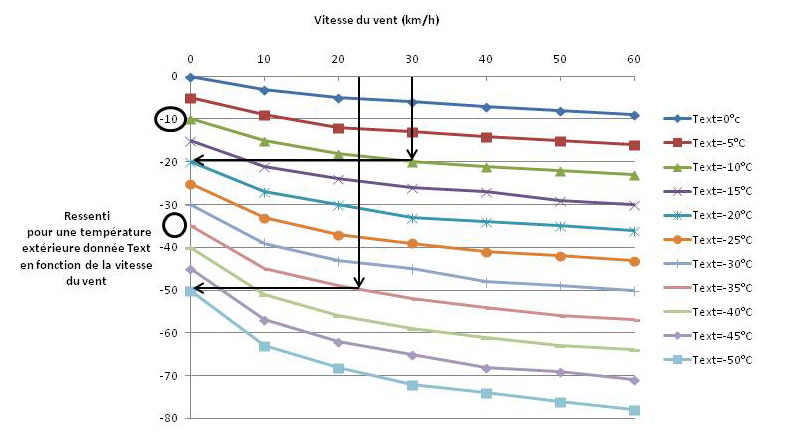
Il faut noter qu'il n'est question ici que de sensation physiologique, la température de la peau n'apparait pas explicitement.
L'article donne les origines de cette correction, au départ essentiellement empirique.
Pour comprendre cette notion Il faut l'analyser à l'aide des outils et des modèles à disposition des physiciens : la diffusion de l'énergie dans un milieu solide (loi de Fourier), les échanges à l'interface solide/gaz, la notion de couche limite dans un écoulement (CL) ...
L'article donne les origines de cette correction, au départ essentiellement empirique.
Pour comprendre cette notion Il faut l'analyser à l'aide des outils et des modèles à disposition des physiciens : la diffusion de l'énergie dans un milieu solide (loi de Fourier), les échanges à l'interface solide/gaz, la notion de couche limite dans un écoulement (CL) ...
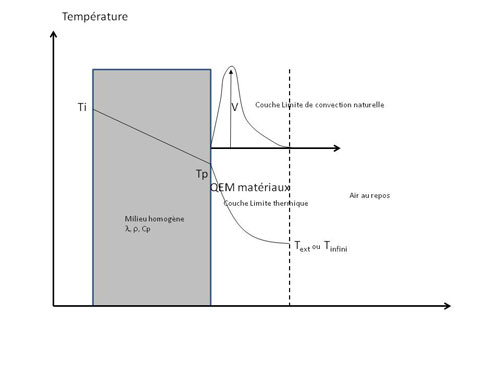
Les échanges de chaleur entre la paroi d'un milieu solide avec l'air extérieur, en régime permanent et en l'absence d'une convection forcée (vent=0), peuvent s'illustrer ainsi ...
On suppose Ti et Text imposées.
On note que le gradient de température n'est pas linéaire dans l'air à proximité de la paroi car se développe là une convection dite naturelle et la naissance d'un couche limite avec un gradient de vitesse, nulle en paroi, maximum au centre et qui retombe vers 0 (limite des effets de la poussée d'Archimède)
A l'équilibre, la température Tp est définie par l'équation de conservation de l'énergie, le bilan peut être défini par :
-λ.(Tp - Ti)/e = h.(Tp - Te) [1]
où :
On note que le gradient de température n'est pas linéaire dans l'air à proximité de la paroi car se développe là une convection dite naturelle et la naissance d'un couche limite avec un gradient de vitesse, nulle en paroi, maximum au centre et qui retombe vers 0 (limite des effets de la poussée d'Archimède)
A l'équilibre, la température Tp est définie par l'équation de conservation de l'énergie, le bilan peut être défini par :
-λ.(Tp - Ti)/e = h.(Tp - Te) [1]
où :
- e/λ représente la résistance thermique du milieu
- h est le coefficient d'échange radiato-convectif en paroi
- Ti et Text sont imposées (hypothèse)
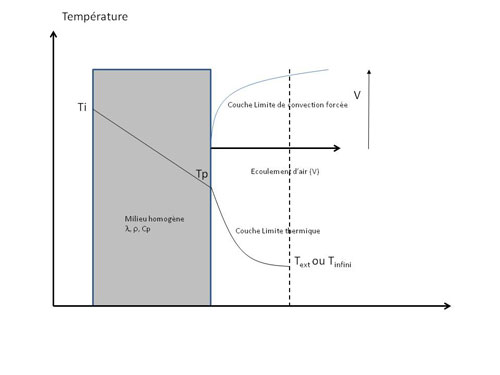
Par contre en cas d'apparition d'une convection forcée (V non nulle), cette configuration est en quelque sorte balayée.
Le régime permanent est rompu, avec apparition d'un transitoire plus ou moins long, les échanges de chaleur entre la paroi et l'air extérieur sont régis par de nouvelles lois.
La couche limite aérodynamique est beaucoup plus dense et active.
En première approximation, après retour à un régime permanent, la même relation [1] peut exprimer l'échange entre paroi et air.
Mais le coefficient h est très différent (h=hcf) ...
Le régime permanent est rompu, avec apparition d'un transitoire plus ou moins long, les échanges de chaleur entre la paroi et l'air extérieur sont régis par de nouvelles lois.
La couche limite aérodynamique est beaucoup plus dense et active.
En première approximation, après retour à un régime permanent, la même relation [1] peut exprimer l'échange entre paroi et air.
Mais le coefficient h est très différent (h=hcf) ...
Dans les deux cas (convection naturelle et forcée) le coefficient d'échange h (hcn et hcf) peut être estimé :
- - en convection naturelle, le nombre de Grashof (Gr) permet de déterminer le régime (laminaire ou turbulent). Le nombre de Nusselt Nu=Lref.h/λ s'exprime à partir de formules empiriques de la forme k.[Gr.Pr]q où Pr est le nombre de Prandtl, k une constante, q un nombre réel [0,1].
D'où l'on déduit h, puis Tp
- - c'est le même type d'approche en convection forcée avec des relations différentes faisant intervenir successivement les nombres de Re, Pr et Nu.
A ce stade, l'idée d'arriver à estimer une température de paroi Tp pour, par exemple, le cas vu précédemment :
Que signifie ressenti ? Est-ce vraiment la température de paroi (peau) ? Est-elle égale dans les deux cas ?
Dans la réalité, les hypothèses proposées ici sont trop simplificatrices : effet transitoire non pris en compte quand V=0 >> V, évaporation de la peau, refroidissement local avec effet de puits un peu comme dans le cas de la mise en contact de deux matériaux (voir ici).
Une analyse plus fine reste à mener ...
- Text=-10°C, V=30km/hoù le ressenti serait le même, s'avère difficile, pour ne pas dire hasardeuse ...
- Text=-20°C, V=0
Que signifie ressenti ? Est-ce vraiment la température de paroi (peau) ? Est-elle égale dans les deux cas ?
Dans la réalité, les hypothèses proposées ici sont trop simplificatrices : effet transitoire non pris en compte quand V=0 >> V, évaporation de la peau, refroidissement local avec effet de puits un peu comme dans le cas de la mise en contact de deux matériaux (voir ici).
Une analyse plus fine reste à mener ...
↑ Haut de page ↑
Le 01.07.2016
Simulations : pour aller plus loin
Soyons fou (en 24 pages) : pour ceux que cela intéresse, une digression sur la réponse thermique d'un empilement, cette fois-ci 3 matériaux, avec une approche simplifiée de régulation.
Vanité humaine, alors qu'il existe un grand nombre de logiciels, certes boites noires, qui font ...1000 fois mieux aujourd'hui !
C'est donc certain : peut encore mieux faire .... mais là il faudra se poser sérieusement la question : que veuille-je faire ?
Vanité humaine, alors qu'il existe un grand nombre de logiciels, certes boites noires, qui font ...1000 fois mieux aujourd'hui !
C'est donc certain : peut encore mieux faire .... mais là il faudra se poser sérieusement la question : que veuille-je faire ?

↑ Haut de page ↑
Le 09.05.2016
Simulations PTE/PTI
Comme annoncé à la rubrique précédente, la réponse thermique en transitoire d'un empilement Isolant+ Conducteur a été réalisée.
Le modèle se décline de deux manières :
- Empilement (extérieur-Isolant/Conducteur-intérieur),noté IC
- Empilement (extérieur-Conducteur/Isolant-intérieur),noté CI
Le contact conducteur/isolant est considéré comme parfait (pas de résistance thermique).
Matériaux :
Isolant : polystyrène, épaisseur 20cm,
Condition initiale T=10°C dans les deux matériaux.
Et avec les Conditions Limites (CL) (type Neumann) suivantes :
En monodimensionnel l’équation de la chaleur, sans source de chaleur interne, se réduit à :
La méthode utilisée pour résoudre cette équation est explicitée en détail ici. Ce n'est pas le sujet ici où nous donnons uniquement les résultats.
Le modèle se décline de deux manières :
- Empilement (extérieur-Isolant/Conducteur-intérieur),noté IC
- Empilement (extérieur-Conducteur/Isolant-intérieur),noté CI
Le contact conducteur/isolant est considéré comme parfait (pas de résistance thermique).
Matériaux :
Isolant : polystyrène, épaisseur 20cm,
a (diffusivité)=1,2.10-6 m2/sConducteur : béton, épaisseur 12cm,
a=9.10-7 m2/s
Condition initiale T=10°C dans les deux matériaux.
Et avec les Conditions Limites (CL) (type Neumann) suivantes :
- Extérieur : flux solaire (Fs) et flux convectif (Fc) périodiques (période T de 24h)
Fs=C.sin(2.π.t/T)
C=400W/m2Et sin(2.π.t/T) imposé à 0 si sinus négatif (pas de flux solaire pour une ½ période correspondant à la nuit)
Fc=he.(Tpext(t)-Te(t)) avec
he=20W/m2/°CTpext(t) : inconnue, température de paroi du mur coté extérieurTe(t)=Tinit+ΔT0.sin(2.π.t/T)
Tinit=10°CΔT0=10°C
La température Te varie sinusoïdalement de +/- 10°C autour de la valeur moyenne de 10°C (conditions un peu sévères mais démonstratives).
Dans notre hypothèse, on notera que les deux flux périodiques sont synchrones : dans la réalité la température extérieure peut encore évoluer (inertie du sol) alors que le soleil est déjà couché. Pour la démonstration l’hypothèse retenue est suffisante, mais le déphasage des deux sources pourrait être facilement réalisé …
- Intérieur : flux (Frc) radiato-convectif
Frc=(hc+hr)(Ti-Tpint(t))
Ti=20°C (température imposée dans la pièce)Tpint(t) : inconnue, température de paroi du mur coté intérieurhc=10W/m2/°Chr=4.ε.σ.Ti3, linéarisation du flux radiatif échangé entre parois en considérant que Ti voisin de Tpint
ε : émissivité, prise égale à 1σ : constante de Stefan : 5,67.10-8 W/m2/K4
Tout l’intérêt de la simulation est de montrer la différence de comportement des 2 empilements en régime transitoire.
En monodimensionnel l’équation de la chaleur, sans source de chaleur interne, se réduit à :
δT(t,x)/δt=a.δ2T(x,t)/δx2
La méthode utilisée pour résoudre cette équation est explicitée en détail ici. Ce n'est pas le sujet ici où nous donnons uniquement les résultats.
1er cas CI : extérieur>>Conducteur/Isolant<<intérieur
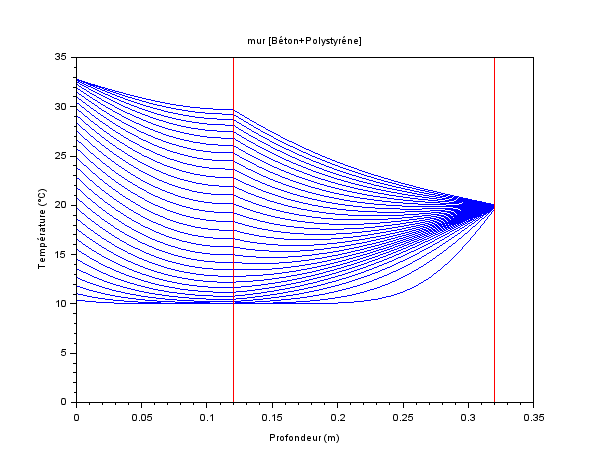
Les répartitions de températures dans les murs sont tracées toutes les 1/4h.
(La répartition spatiale de température à un temps donné s'appelle une isochrone).
Le calcul a été arrêté à t0+8h (32 isochrones).
Que voit-on ?
On démarre bien de 10°c (courbe du bas) mais le modèle répond rapidement aux CL qu’on lui impose, en particulier coté intérieur où la paroi est soumise dès t+dt à un flux instantané de #150W/m2 (température imposée de 20°C).
Coté extérieur, le flux reçu varie plus doucement, tempéré par la fonction périodique.
On notera au passage la discontinuité au contact (1er trait rouge) : les densités de flux sont bien égales (-λ1δT/δx1=-λ2δT/δx2) mais les propriétés étant différentes, les gradients le sont aussi.
Autre constat : le béton, conducteur, réagit assez rapidement au flux entrant.
(La répartition spatiale de température à un temps donné s'appelle une isochrone).
Le calcul a été arrêté à t0+8h (32 isochrones).
Que voit-on ?
On démarre bien de 10°c (courbe du bas) mais le modèle répond rapidement aux CL qu’on lui impose, en particulier coté intérieur où la paroi est soumise dès t+dt à un flux instantané de #150W/m2 (température imposée de 20°C).
Coté extérieur, le flux reçu varie plus doucement, tempéré par la fonction périodique.
On notera au passage la discontinuité au contact (1er trait rouge) : les densités de flux sont bien égales (-λ1δT/δx1=-λ2δT/δx2) mais les propriétés étant différentes, les gradients le sont aussi.
Autre constat : le béton, conducteur, réagit assez rapidement au flux entrant.
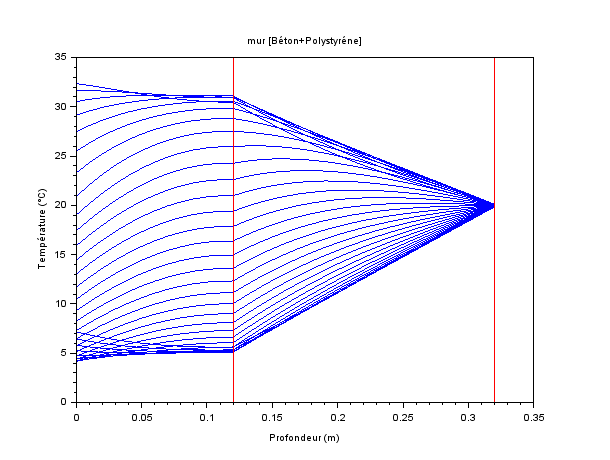
Calcul entre t0+8h et t0+24h.
Tracés toutes les 1/2h (32 isochrones).
A partir de t0+12h le flux solaire est nul, ce qui accélère la baisse du gradient dans le béton.
Début de remontée vers t0+21h car le flux convectif 'repart' (depuis t0+18h).
Tracés toutes les 1/2h (32 isochrones).
A partir de t0+12h le flux solaire est nul, ce qui accélère la baisse du gradient dans le béton.
Début de remontée vers t0+21h car le flux convectif 'repart' (depuis t0+18h).
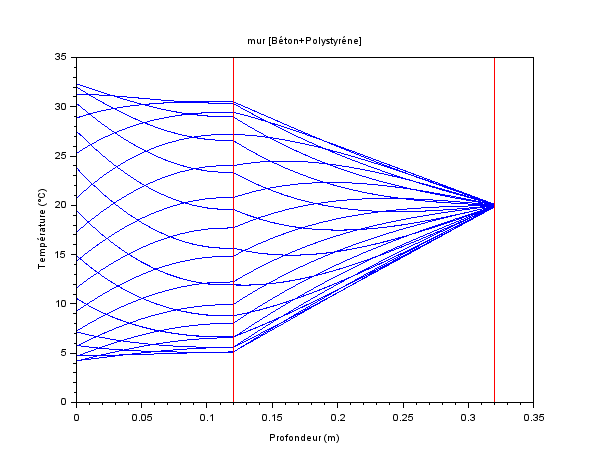
Calcul entre t0+24h et t0+3jours.
Tracés toutes les heures.
Les isochrones ont ‘remonté ‘puis ‘redescendu’ (influence de la CL extérieure).
Il y a 48 isochrones tracées mais leur nombre parait moins important sur le graphique.
En fait les Conditions Limites périodiques conduisent, après un court régime transitoire, à l’établissement d’un pseudo régime permanent périodique.
Mais la variabilité des CL fait qu’on atteint jamais un vrai régime permanent (pour lequel le gradient serait linéaire dans chaque matériau).
Tracés toutes les heures.
Les isochrones ont ‘remonté ‘puis ‘redescendu’ (influence de la CL extérieure).
Il y a 48 isochrones tracées mais leur nombre parait moins important sur le graphique.
En fait les Conditions Limites périodiques conduisent, après un court régime transitoire, à l’établissement d’un pseudo régime permanent périodique.
Mais la variabilité des CL fait qu’on atteint jamais un vrai régime permanent (pour lequel le gradient serait linéaire dans chaque matériau).
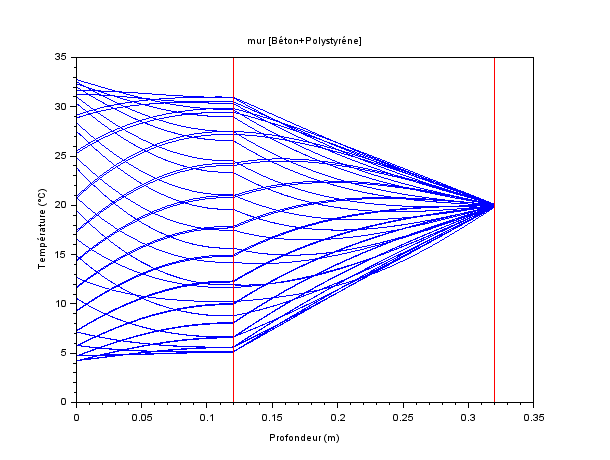
Ceci est vérifié en relançant un calcul depuis t0 sur plusieurs périodes, par exemple 6, soit 6 jours.
Tracés toutes les heures.
Les isochrones déterminent un domaine qui reste constant.
De plus chaque isochrone converge vers une valeur fixe à T près (période de 24h). Les courbes se superposent et s’épaississent.
A noter, à la paroi du polystyrène coté intérieur, le flux est piloté par la température imposée dans la pièce (20°C) : pour les deux gradients déterminant les limites basses et hautes du domaine de variation de la température il vaut # ±2 W/m2.
L’idéal serait de tracer ce réseau en dynamique comme cela le fait à l’affichage pendant le calcul : c’est réalisable mais cela demanderait un peu d’investissement …
Tracés toutes les heures.
Les isochrones déterminent un domaine qui reste constant.
De plus chaque isochrone converge vers une valeur fixe à T près (période de 24h). Les courbes se superposent et s’épaississent.
A noter, à la paroi du polystyrène coté intérieur, le flux est piloté par la température imposée dans la pièce (20°C) : pour les deux gradients déterminant les limites basses et hautes du domaine de variation de la température il vaut # ±2 W/m2.
L’idéal serait de tracer ce réseau en dynamique comme cela le fait à l’affichage pendant le calcul : c’est réalisable mais cela demanderait un peu d’investissement …
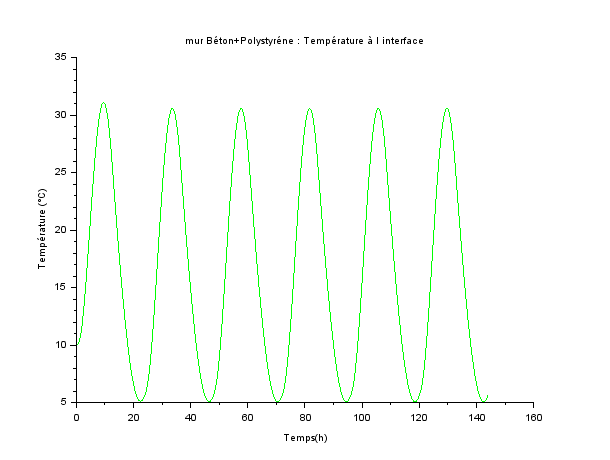
Le régime périodique établi est encore plus visible si on trace l’évolution de la température de l’interface béton/polystyrène en fonction du temps.
La simulation est faite sur 6 jours.
La période de 24h est bien visible.
On peut s’étonner que la température de paroi coté extérieur ne descende jamais au voisinage de 0°C alors que la température extérieure fluctue sinusoïdalement entre ±10°C autour de la valeur moyenne 10°C : l’énergie solaire emmagasinée le jour joue un rôle de tampon régulateur dans le mur.
La simulation est faite sur 6 jours.
La période de 24h est bien visible.
On peut s’étonner que la température de paroi coté extérieur ne descende jamais au voisinage de 0°C alors que la température extérieure fluctue sinusoïdalement entre ±10°C autour de la valeur moyenne 10°C : l’énergie solaire emmagasinée le jour joue un rôle de tampon régulateur dans le mur.
2ème cas IC : extérieur>>Isolant/Conducteur<<intérieur
Les répartitions de températures dans les murs sont tracées toutes les 1/4h.
Le calcul a été arrêté à t0+8h.
(32 isochrones tracées)
A noter l'évolution de température externe de l'isolant qui réagit quasi-instantanément à la C.L. (faible conductivité).
Le calcul a été arrêté à t0+8h.
(32 isochrones tracées)
A noter l'évolution de température externe de l'isolant qui réagit quasi-instantanément à la C.L. (faible conductivité).
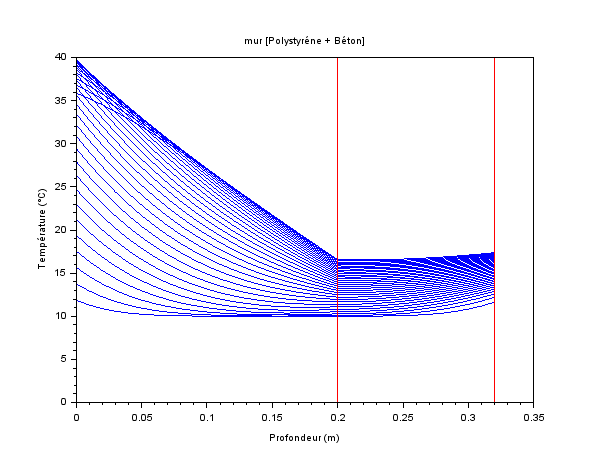
Calcul entre t0+8h et t0+24h.
Tracés toutes les 1/2h (soit 32 isochrones).
Depuis t0+12h le flux solaire est nul.
La température extérieure coté isolant suit quasiment la CL : ici l’amplitude de ±10°C est visible, l’isolant jour son rôle (elle va au-delà des 20°C avec l’apport solaire).
On constate déjà que le béton est presque isotherme, avec une faible variation de température.
Tracés toutes les 1/2h (soit 32 isochrones).
Depuis t0+12h le flux solaire est nul.
La température extérieure coté isolant suit quasiment la CL : ici l’amplitude de ±10°C est visible, l’isolant jour son rôle (elle va au-delà des 20°C avec l’apport solaire).
On constate déjà que le béton est presque isotherme, avec une faible variation de température.
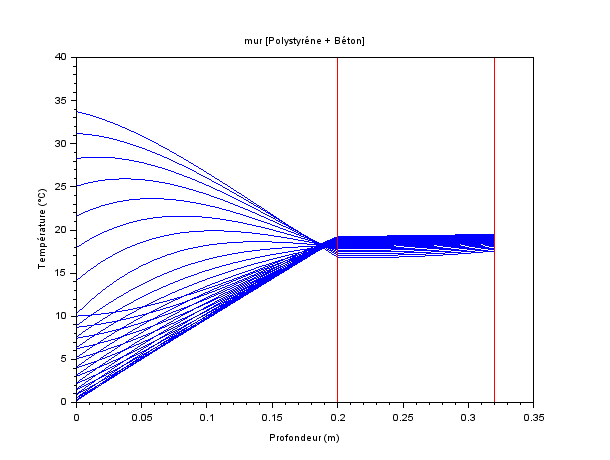
Calcul entre t0+24h et t0+3jours.
Tracés toutes les heures.
Les isochrones dans l’isolant ont ‘remonté ‘puis ‘redescendu’.
Il y a 48 isochrones tracées mais leur nombre parait moins important sur le graphique.
Ici dans l’isolant les Conditions Limites périodiques conduisent, après un court régime transitoire, à l’établissement d’un pseudo régime permanent périodique.
Mais la variabilité de la CL fait qu’on atteint jamais un vrai régime permanent (le gradient n’est pas linéaire).
Par contre la température dans le béton est déjà quasiment stable et constante.
Tracés toutes les heures.
Les isochrones dans l’isolant ont ‘remonté ‘puis ‘redescendu’.
Il y a 48 isochrones tracées mais leur nombre parait moins important sur le graphique.
Ici dans l’isolant les Conditions Limites périodiques conduisent, après un court régime transitoire, à l’établissement d’un pseudo régime permanent périodique.
Mais la variabilité de la CL fait qu’on atteint jamais un vrai régime permanent (le gradient n’est pas linéaire).
Par contre la température dans le béton est déjà quasiment stable et constante.
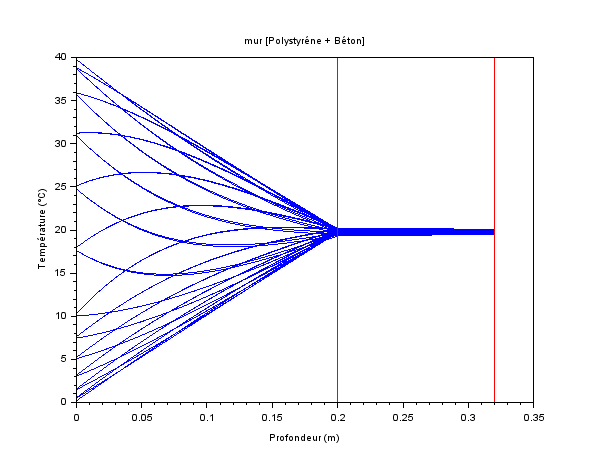
La vue d’ensemble est obtenue en relançant un calcul depuis t0 sur plusieurs périodes, par exemple 6, soit 6 jours.
Tracés toutes les heures.
Coté isolant, chaque isochrone converge vers une valeur fixe à T près (période de 24h). Les courbes se superposent.
Tracés toutes les heures.
Coté isolant, chaque isochrone converge vers une valeur fixe à T près (période de 24h). Les courbes se superposent.
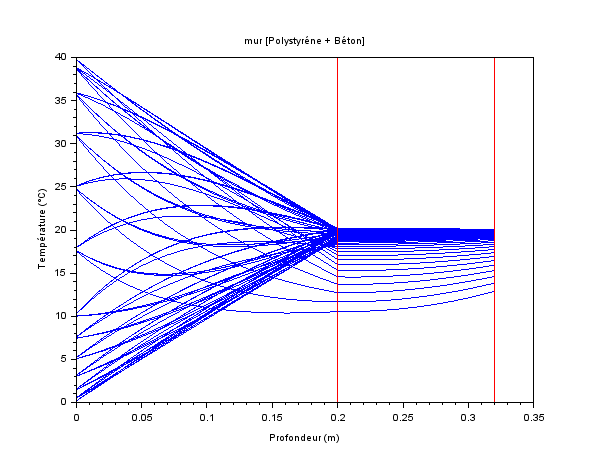
Ce régime périodique établi est aussi très visible si on trace l’évolution de la température de l’interface béton/polystyrène en fonction du temps.
La simulation est faite sur 6 jours.
La réalité du régime vraiment transitoire, depuis la condition initiale de température, apparait ici : une trentaine d'heures.
La température du béton varie peu, contrairement au cas de la simulation CI, mais toujours de manière périodique (on retrouve bien la période, longue, de 24h).
A la fin du calcul (régime quasi permanent dans le béton) le flux traversant l’épaisseur de béton, comme dans la simulation CI, vaut #2,3W/m2.
La simulation est faite sur 6 jours.
La réalité du régime vraiment transitoire, depuis la condition initiale de température, apparait ici : une trentaine d'heures.
La température du béton varie peu, contrairement au cas de la simulation CI, mais toujours de manière périodique (on retrouve bien la période, longue, de 24h).
A la fin du calcul (régime quasi permanent dans le béton) le flux traversant l’épaisseur de béton, comme dans la simulation CI, vaut #2,3W/m2.
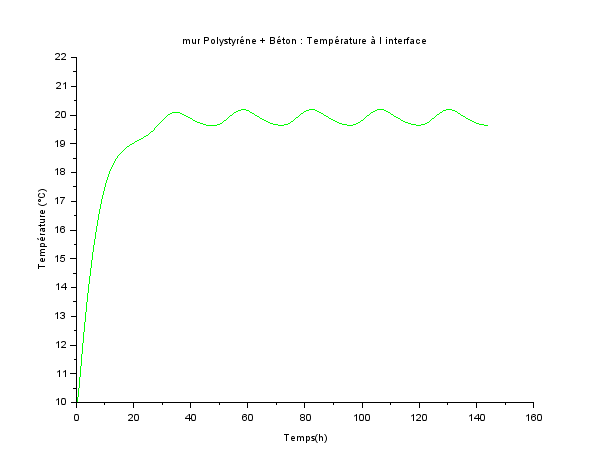
Ce qu'il faut retenir de ce cas d'école :
- la température de l'interface est beaucoup moins sensible au caractère périodique des CL externes dans le cas IC (# 1/2°C) par rapport au cas CI (# 25°C).
- en conséquence la température de paroi du mur intérieur en béton (cas IC) est quasi stationnaire quand le régime sinusoidal a dépassé ne serait-ce qu'une période : cette stabilité est synonyme de confort.
- le mur intérieur conducteur (IC) stocke l'énergie et jour le role de régulateur lors du passage d'un épisode froid à un épisode chaud.
↑ Haut de page ↑
Le 22.04.2016
Protection Thermique Interne ou Protection Thermique Externe ?
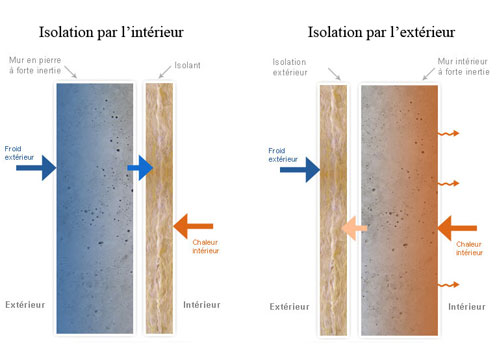
Question qui revient de manière récurrente dans l'habitat : faut-il isoler par l'extérieur ou par l'intérieur, quelle est la différence, et sur quels critères faire le choix.
Le tableau ci-dessous présente les arguments pour et contre pour chaque solution.
Certains arguments sont évidents et factuels.
Le tableau ci-dessous présente les arguments pour et contre pour chaque solution.
Certains arguments sont évidents et factuels.

Credit mamaisonbioclimatique
Le résultat de l’analyse de chaque solution montre que la PTE est la solution favorable, en particulier pour la rénovation (exception faite des bâtiments présentant un intérêt architectural).
Pour le neuf, je n’ai pas encore trouvé la démonstration formelle et la confirmation du bienfait de l’utilisation de nouveaux matériaux (mono-mur brique, béton cellulaire), isolant et structure à la fois qui ont un surcout non négligeable et qui demandent un soin tout particulier au montage.
Pour le neuf, je n’ai pas encore trouvé la démonstration formelle et la confirmation du bienfait de l’utilisation de nouveaux matériaux (mono-mur brique, béton cellulaire), isolant et structure à la fois qui ont un surcout non négligeable et qui demandent un soin tout particulier au montage.
Je me proposais de refaire la démonstration quantifiée du gain de performance thermique, pour les deux cas d'assemblage mur/isolant en PTE ou PTI.
Pour ce faire, petit retour en arrière incontournable dans les mécanismes de transfert d'énergie et des équations qui les gouvernent.
Par exemple avec l'équation généralisée de la chaleur :
div(λ.grad T) - ρ.Cp.δT/δt = -P [1] où T est fonction de l'espace (3D) et du temps (t).
Cette équation se simplifie largement pour notre application :
[1] devient :
ΔT = 1/a. δT/δt [2]
a : diffusivité (m2/s), a=λ/(ρ.Cp), caractérise la propagation du signal thermique dans le milieu (grande si la conductivité λ est importante et si la chaleur massique ρ.Cp est faible)
Cette équation a de nombreuses solutions analytiques répertoriées.
Il y a plus de 40 ans nous utilisions quelques ouvrages de référence comme le CARSLAW & JAEGER ou le KREITH.
Aujourd'hui ces informations sont disponibles sur de nombreux sites, comme celui-ci d'où j'ai extrait les cas qui pouvaient nous intéresser.
Ces solutions sont différenciées entre elles par les conditions limites (CL) affectées au système : et c'est souvent là que la réalité se heurte à la fiction.
En 1D instationnaire (régime d'équilibre non établi) elles concernent souvent un milieu semi infini (CL de température imposée constante ou périodique ou de flux imposé) ou un mur mono-matériau (CL idem).
Le Dirac de température (CL très très conservatoire et difficile à réaliser) sur la face d'un milieu semi-infini est l'un des plus connu : la solution s'exprime par :
T(x,t)= T0. erf[x/2/(at)1/2]
avec :
T(x,0)=T0, la température est uniforme (T0) dans tout le matériau à l'instant initial.
T(0,t)=0, c'est à dire qu'on impose la température T=0 en x=0, à partir de t=0
(Pour ceux qui veulent approfondir, erf(x)= 2/π1/2.ʃ0x exp(-u2).du, voir le lien).
Hélas cette solution ne s'applique pas à notre cas (milieu fini, 2 matériaux). Tout au plus pouvons-nous regarder la propagation de l'onde thermique jusqu'à ce qu'elle atteigne l'épaisseur (e) du premier mur (et pas plus!), par exemple T(x=e,t)#99,9%T0 (soit erf()=0,999...).
Tout calcul fait, à la profondeur e, la température, initialement à T0, baisse de 1‰ au temps t= x2/(36a).
Le temps de propagation de l'onde thermique est inversement proportionnel à la diffusivité (logique !).
Pour ces deux matériaux :
Pour ce faire, petit retour en arrière incontournable dans les mécanismes de transfert d'énergie et des équations qui les gouvernent.
Par exemple avec l'équation généralisée de la chaleur :
div(λ.grad T) - ρ.Cp.δT/δt = -P [1] où T est fonction de l'espace (3D) et du temps (t).
Cette équation se simplifie largement pour notre application :
- milieu homogène et isotrope,
- milieu 1D (une seule dimension de propagation x),
- propriétés des matériaux indépendantes de la température,
- pas de production d'énergie au sein du milieu.
[1] devient :
ΔT = 1/a. δT/δt [2]
a : diffusivité (m2/s), a=λ/(ρ.Cp), caractérise la propagation du signal thermique dans le milieu (grande si la conductivité λ est importante et si la chaleur massique ρ.Cp est faible)
Cette équation a de nombreuses solutions analytiques répertoriées.
Il y a plus de 40 ans nous utilisions quelques ouvrages de référence comme le CARSLAW & JAEGER ou le KREITH.
Aujourd'hui ces informations sont disponibles sur de nombreux sites, comme celui-ci d'où j'ai extrait les cas qui pouvaient nous intéresser.
Ces solutions sont différenciées entre elles par les conditions limites (CL) affectées au système : et c'est souvent là que la réalité se heurte à la fiction.
En 1D instationnaire (régime d'équilibre non établi) elles concernent souvent un milieu semi infini (CL de température imposée constante ou périodique ou de flux imposé) ou un mur mono-matériau (CL idem).
Le Dirac de température (CL très très conservatoire et difficile à réaliser) sur la face d'un milieu semi-infini est l'un des plus connu : la solution s'exprime par :
T(x,t)= T0. erf[x/2/(at)1/2]
avec :
T(x,0)=T0, la température est uniforme (T0) dans tout le matériau à l'instant initial.
T(0,t)=0, c'est à dire qu'on impose la température T=0 en x=0, à partir de t=0
(Pour ceux qui veulent approfondir, erf(x)= 2/π1/2.ʃ0x exp(-u2).du, voir le lien).
Hélas cette solution ne s'applique pas à notre cas (milieu fini, 2 matériaux). Tout au plus pouvons-nous regarder la propagation de l'onde thermique jusqu'à ce qu'elle atteigne l'épaisseur (e) du premier mur (et pas plus!), par exemple T(x=e,t)#99,9%T0 (soit erf()=0,999...).
Tout calcul fait, à la profondeur e, la température, initialement à T0, baisse de 1‰ au temps t= x2/(36a).
Le temps de propagation de l'onde thermique est inversement proportionnel à la diffusivité (logique !).
Pour ces deux matériaux :

t vaut presque 9mn pour le polystyrène (15cm), et 5mn pour le béton (10cm). La propagation de la perturbation est très rapide, même dans l'isolant.
L'écart peut sembler faible mais en fait les diffusivités des deux matériaux ne sont pas si éloignées : le béton compense sa grande conductivité par sa capacité à stocker la chaleur (forte chaleur massique ρ.Cp).
Ce cas d'école n'apporte pas d'élément probant quant au choix PTE/PTI ...!
L'écart peut sembler faible mais en fait les diffusivités des deux matériaux ne sont pas si éloignées : le béton compense sa grande conductivité par sa capacité à stocker la chaleur (forte chaleur massique ρ.Cp).
Ce cas d'école n'apporte pas d'élément probant quant au choix PTE/PTI ...!
Le cas encore plus simple en régime permanent (ou régime établi) fait appel à la loi de Fourier. A l'équilibre, le flux Φ (W) qui traverse une surface S de mur s'écrit :
Φ= λ/e.S.(Ti-Te) [3]
Soit notre mur composé des 2 matériaux précités (PTE polystyrène + mur en béton), en contact parfait (hypothèse simplificatrice qui ne remet pas en cause le principe de la démonstration).
A l'équilibre nous pouvons écrire pour chacun des matériaux :
Φ1= λ1/e1.S.(Tc-Te)
Φ2= λ2/e2.S.(Ti-Tc)
D'après le principe de conservation de l'énergie Φ1= Φ2 (en densité de flux)
Soit :
Tc = Te.h1+Ti.h2/(h1+h2) avec hi=λi/ei, i=1,2
Φ= λ/e.S.(Ti-Te) [3]
Soit notre mur composé des 2 matériaux précités (PTE polystyrène + mur en béton), en contact parfait (hypothèse simplificatrice qui ne remet pas en cause le principe de la démonstration).
A l'équilibre nous pouvons écrire pour chacun des matériaux :
Φ1= λ1/e1.S.(Tc-Te)
Φ2= λ2/e2.S.(Ti-Tc)
D'après le principe de conservation de l'énergie Φ1= Φ2 (en densité de flux)
Soit :
Tc = Te.h1+Ti.h2/(h1+h2) avec hi=λi/ei, i=1,2
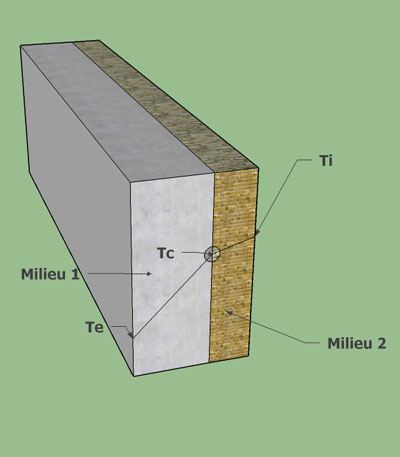
Imposons les CL :
- Te = 0°C (air extérieur)
- Ti = 20°C (intérieur habitat)
Résultat :
Tc=19,3 °C isolant extérieur
Tc=0,3 °C isolant intérieur
Tc=19,3 °C isolant extérieur
Tc=0,3 °C isolant intérieur
Le béton, qui a une conductivité presque 50 fois plus élevée que celle du polystyrène, est presque isotherme, le polystyrène assume l'essentiel du gradient de température. Mais c'est tout....
Comme nous le constatons la comparaison quantifiée de notre mur + PTE ou + PTI n'est pas probante à ce stade !!
L'équation de la chaleur n'a pas de solution analytique pour ce cas d'empilement en régime transitoire (étude de la réponse des matériaux), qui plus est avec des CL réalistes (Température ou flux fonctions du temps, voire +).
Quid ? Il faut faire appel à l'analyse numérique qui permet d'évaluer numériquement une fonction (ici l'équation aux dérivées partielles de la chaleur) via quelques méthodes issues des mathématiques.
Les plus connues sont :
Pour ce cas d'école (2 matériaux, 1D, transitoire, CL variées), qui a du faire l'objet de nombreux codes de calcul, je n'ai pas retrouvé de logiciel libre (gratuit!) me permettant de répondre à notre préoccupation.
Ce sera donc la prochaine étape, refaire cet algorithme !
L'équation de la chaleur n'a pas de solution analytique pour ce cas d'empilement en régime transitoire (étude de la réponse des matériaux), qui plus est avec des CL réalistes (Température ou flux fonctions du temps, voire +).
Quid ? Il faut faire appel à l'analyse numérique qui permet d'évaluer numériquement une fonction (ici l'équation aux dérivées partielles de la chaleur) via quelques méthodes issues des mathématiques.
Les plus connues sont :
- les différences finies (méthode la plus facile d'accès mais limitée)
- les volumes finis (approche physique des phénomènes)
- les éléments finis généralisées maintenant à tous les domaines de la physique
Pour ce cas d'école (2 matériaux, 1D, transitoire, CL variées), qui a du faire l'objet de nombreux codes de calcul, je n'ai pas retrouvé de logiciel libre (gratuit!) me permettant de répondre à notre préoccupation.
Ce sera donc la prochaine étape, refaire cet algorithme !
↑ Haut de page ↑
Le 20.04.2015
L'énergie solaire
L’énergie solaire a fait l’objet d’un vif intérêt dès le milieu des années 1970, juste après le premier choc pétrolier.
Dommage que le cours du baril de pétrole ait rechuté dans le milieu des années 1980 : cet intérêt est retombé aussi vite …
L’énergie solaire a fait l’objet d’un vif intérêt dès le milieu des années 1970, juste après le premier choc pétrolier.
Dommage que le cours du baril de pétrole ait rechuté dans le milieu des années 1980 : cet intérêt est retombé aussi vite …
A cette époque l’ONERA menait des essais de tenue à haute température de matériaux réfractaires au four solaire d’Odeillo, essais auxquels j’ai participé.
L’effet Trombe, du nom de son inventeur, était déjà mis en pratique dans les bâtiments administratifs attenants au four. Le principe en est très bien expliqué.
C’est la version historique du four solaire, servant quasiment exclusivement à la Recherche.
La centrale solaire THEMIS a vu le jour quelques années plus tard (1983). Après un arrêt prolongé pour raisons techniques, son exploitation a repris : un programme de recherche sur la production d’électricité par un système hybride solaire/gaz est en cours.
Depuis une quinzaine d’année les applications de l’énergie solaire pour les particuliers se sont développées, en grande partie grâce aux aides du crédit d’impôt (pour mémoire voir ce récapitulatif).
Deux voies sont explorées : énergie photovoltaïque et énergie thermique.
Nous y reviendrons.
L’effet Trombe, du nom de son inventeur, était déjà mis en pratique dans les bâtiments administratifs attenants au four. Le principe en est très bien expliqué.
C’est la version historique du four solaire, servant quasiment exclusivement à la Recherche.
La centrale solaire THEMIS a vu le jour quelques années plus tard (1983). Après un arrêt prolongé pour raisons techniques, son exploitation a repris : un programme de recherche sur la production d’électricité par un système hybride solaire/gaz est en cours.
Depuis une quinzaine d’année les applications de l’énergie solaire pour les particuliers se sont développées, en grande partie grâce aux aides du crédit d’impôt (pour mémoire voir ce récapitulatif).
Deux voies sont explorées : énergie photovoltaïque et énergie thermique.
Nous y reviendrons.
Crédit CNRS Odeillo

↑ Haut de page ↑
Le 19.04.2015
Notions fondamentales
Le Joule (J) est l’unité de mesure d’énergie : 1 J équivaut au travail produit par une force de 1N dont le point d’application de déplace d’1mètre dans la direction de la force.
Ainsi avec une corde accrochée à une poulie, soulever de 2m une masse de 100kg, soit une force de 1000N (pesanteur), nécessite de fournir une énergie de 2000J (1000x2).
Le Watt (W) est une unité de puissance : 1W est la puissance d’un système dans lequel l’énergie d’1 Joule est transférée en 1 seconde (1W ~ 1J/s, énergie par unité de temps).
Toujours avec cette même poulie et ce même poids, le levage d’une durée de 2s correspond à une puissance développée de 1000W (2000/2).
Si vous êtes très costaud (plus forte puissance disponible) vous pouvez aussi le faire en moins de 2s ….
Plus cette durée est longue, plus la puissance (énergie par unité de temps) nécessaire est faible.
Mais l’énergie globale à fournir (2000J) sera toujours la même.
L’énergie peut être appréhendée de différentes manières : énergie mécanique, électrique, hydraulique, calorifique, …
Pour cette dernière, c’est J.P. Joule qui démontra le premier l’équivalence entre énergie mécanique et chaleur : 1cal # 4,18J (Principe d’équivalence).
La calorie étant parfaitement définie par ailleurs : c’est la quantité de chaleur nécessaire pour élever la température d’1 g d’eau de 1°C (chaleur spécifique de l’eau).
Ainsi le bassin d’une piscine de 50m (largeur 20m, profondeur 2m) dont l’eau, initialement à 15°C sur le réseau, est chauffée à 25°C nécessite l’apport initial de 2.1010 calories soit 8,36.1010 J !
V=50x20x2= 2000 m3 = 2. 106 dm3 ou litres
Soit M= 2. 106 kg soit 2.109g.
Cpeau=1 cal/g
ΔT = 10°C
E=M.Cp.ΔT=2.1010 cal !
(Température qu’il faut ensuite maintenir par un apport de chaleur pour compenser les pertes inévitables …Mais ça, c’est autre chose)
Autre unité, le kWh utilisé pour désigner une consommation ou une production.
Equation Dimension : kW.h # W.h # J.h/s # J
C’est donc bien une unité d’énergie, au même titre que le J, utilisée principalement par les fournisseurs d’énergie.
1 kWh = 3 600 000 J
Plus généralement, 1 kWh est l’énergie consommée par un appareil d’une puissance de 1000W pendant une heure.
Une ampoule de 50W allumée pendant 6 heures a consommé 300Wh.
Un rasoir électrique d’une puissance de 10W, utilisé 3mn par jour, consomme annuellement 0.1825 kWh.
Puissance et vitesse sont les dérivées respectives de l’énergie et de la distance par rapport au temps
On peut faire le parallèle suivant :
km (distance parcourue) <> J (énergie totale consommée)
km/h (vitesse à laquelle on ‘consomme’ la distance) <> Puissance (vitesse à laquelle on consomme l’énergie).
Au passage, ne pas confondre avec le kW/h, très peu utilisé (ou alors à mauvais escient, et plutôt à proscrire), simplement pour quantifier des variations temporelles de puissance.
Equation Dimension : J/s2 (dimension d’une accélération d’énergie).
Le Joule (J) est l’unité de mesure d’énergie : 1 J équivaut au travail produit par une force de 1N dont le point d’application de déplace d’1mètre dans la direction de la force.
Ainsi avec une corde accrochée à une poulie, soulever de 2m une masse de 100kg, soit une force de 1000N (pesanteur), nécessite de fournir une énergie de 2000J (1000x2).
Le Watt (W) est une unité de puissance : 1W est la puissance d’un système dans lequel l’énergie d’1 Joule est transférée en 1 seconde (1W ~ 1J/s, énergie par unité de temps).
Toujours avec cette même poulie et ce même poids, le levage d’une durée de 2s correspond à une puissance développée de 1000W (2000/2).
Si vous êtes très costaud (plus forte puissance disponible) vous pouvez aussi le faire en moins de 2s ….
Plus cette durée est longue, plus la puissance (énergie par unité de temps) nécessaire est faible.
Mais l’énergie globale à fournir (2000J) sera toujours la même.
L’énergie peut être appréhendée de différentes manières : énergie mécanique, électrique, hydraulique, calorifique, …
Pour cette dernière, c’est J.P. Joule qui démontra le premier l’équivalence entre énergie mécanique et chaleur : 1cal # 4,18J (Principe d’équivalence).
La calorie étant parfaitement définie par ailleurs : c’est la quantité de chaleur nécessaire pour élever la température d’1 g d’eau de 1°C (chaleur spécifique de l’eau).
Ainsi le bassin d’une piscine de 50m (largeur 20m, profondeur 2m) dont l’eau, initialement à 15°C sur le réseau, est chauffée à 25°C nécessite l’apport initial de 2.1010 calories soit 8,36.1010 J !
V=50x20x2= 2000 m3 = 2. 106 dm3 ou litres
Soit M= 2. 106 kg soit 2.109g.
Cpeau=1 cal/g
ΔT = 10°C
E=M.Cp.ΔT=2.1010 cal !
(Température qu’il faut ensuite maintenir par un apport de chaleur pour compenser les pertes inévitables …Mais ça, c’est autre chose)
Autre unité, le kWh utilisé pour désigner une consommation ou une production.
Equation Dimension : kW.h # W.h # J.h/s # J
C’est donc bien une unité d’énergie, au même titre que le J, utilisée principalement par les fournisseurs d’énergie.
1 kWh = 3 600 000 J
Plus généralement, 1 kWh est l’énergie consommée par un appareil d’une puissance de 1000W pendant une heure.
Une ampoule de 50W allumée pendant 6 heures a consommé 300Wh.
Un rasoir électrique d’une puissance de 10W, utilisé 3mn par jour, consomme annuellement 0.1825 kWh.
Puissance et vitesse sont les dérivées respectives de l’énergie et de la distance par rapport au temps
On peut faire le parallèle suivant :
km (distance parcourue) <> J (énergie totale consommée)
km/h (vitesse à laquelle on ‘consomme’ la distance) <> Puissance (vitesse à laquelle on consomme l’énergie).
Au passage, ne pas confondre avec le kW/h, très peu utilisé (ou alors à mauvais escient, et plutôt à proscrire), simplement pour quantifier des variations temporelles de puissance.
Equation Dimension : J/s2 (dimension d’une accélération d’énergie).
crédit Arts & Métiers

crédit nageurs.com

↑ Haut de page ↑
Le 13.03.2015
Une grandeur physique liée aussi aux transferts de chaleur, peu connue mais qu’il est facile d’appréhender car nous pouvons la ressentir, sans le savoir, dans la vie courant : l’effusivité.
Qu’est-ce ?
Tout le monde a entendu parler de la conductivité thermique d’un matériau (λ) qui est associée à sa faculté de propager plus ou moins la chaleur.
Typiquement le cuivre est très conducteur, le liège l’est beaucoup moins !!
L’équation de Fourrier précise même cette notion en parlant de diffusivité a=λ/(ρ.Cp), avec ρ masse volumique et Cp chaleur spécifique, caractéristique de la diffusion de la chaleur au sein de ce milieu.
L'effusivité est la grandeur physique qui caractérise l’aptitude d’un milieu à échanger de la chaleur avec un autre milieu avec lequel il est mis en contact. Tout est dit dans le mot contact.
Prenons tout de suite un exemple concret : ma température de surface de peau est de l’ordre de 31°C.
La sensation sur mon doigt est très différente si je touche un morceau de métal ou une pièce plastique, pourtant tous deux à la même température uniforme (T ambiante par exemple 20°C) : fraicheur dans le premier cas, plutôt douceur dans le second.
Explication : dans la zone de contact, la température du contact tend vers la température du corps qui a la plus grande effusivité. Ici en l’occurrence le métal.
Cette grandeur, notée historiquement b, est caractérisée par le groupe b=(λ.ρ.Cp)1/2
Nous retrouvons les mêmes caractéristiques du matériau, ordonnées différemment.
Les deux paramètres a et b sont liés par la relation a=[λ/b] 2
Que se passe-t-il au contact ? le métal opère un effet local de puits de chaleur (forte conductivité, forte capacité) et crée un gradient plus important que dans le cas du plastique.
Nous pouvons représenter ce qui se passe ainsi :
Qu’est-ce ?
Tout le monde a entendu parler de la conductivité thermique d’un matériau (λ) qui est associée à sa faculté de propager plus ou moins la chaleur.
Typiquement le cuivre est très conducteur, le liège l’est beaucoup moins !!
L’équation de Fourrier précise même cette notion en parlant de diffusivité a=λ/(ρ.Cp), avec ρ masse volumique et Cp chaleur spécifique, caractéristique de la diffusion de la chaleur au sein de ce milieu.
L'effusivité est la grandeur physique qui caractérise l’aptitude d’un milieu à échanger de la chaleur avec un autre milieu avec lequel il est mis en contact. Tout est dit dans le mot contact.
Prenons tout de suite un exemple concret : ma température de surface de peau est de l’ordre de 31°C.
La sensation sur mon doigt est très différente si je touche un morceau de métal ou une pièce plastique, pourtant tous deux à la même température uniforme (T ambiante par exemple 20°C) : fraicheur dans le premier cas, plutôt douceur dans le second.
Explication : dans la zone de contact, la température du contact tend vers la température du corps qui a la plus grande effusivité. Ici en l’occurrence le métal.
Cette grandeur, notée historiquement b, est caractérisée par le groupe b=(λ.ρ.Cp)1/2
Nous retrouvons les mêmes caractéristiques du matériau, ordonnées différemment.
Les deux paramètres a et b sont liés par la relation a=[λ/b] 2
Que se passe-t-il au contact ? le métal opère un effet local de puits de chaleur (forte conductivité, forte capacité) et crée un gradient plus important que dans le cas du plastique.
Nous pouvons représenter ce qui se passe ainsi :
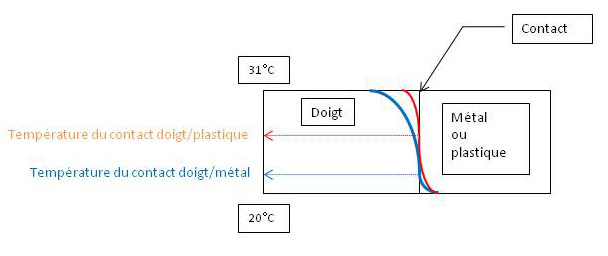
Dans la zone de contact, en rouge la répartition de température dans le cas du plastique, en bleu celle dans le cas du métal.
La théorie montre que la température de contact (Tc) est fonction des effusivités respectives de chaque matériau.
Tc = (b1.T1 + b2.T2)/(b1 + b2)
Sinon, quelle utilité ?
Le choix du doigt dans l'exemple n'est pas anodin : l'effusivité caractérise dans un contact la sensation de chaud ou de froid, le confort d'un matériau est synonyme de faible effusivité.
Voici au lien suivant (extrait thèse) un bel exemple de l'utilisation de ce paramètre [datant un peu, texte tapé à la machine (!), le traitement de texte était à peine né].
La théorie montre que la température de contact (Tc) est fonction des effusivités respectives de chaque matériau.
Tc = (b1.T1 + b2.T2)/(b1 + b2)
Sinon, quelle utilité ?
Le choix du doigt dans l'exemple n'est pas anodin : l'effusivité caractérise dans un contact la sensation de chaud ou de froid, le confort d'un matériau est synonyme de faible effusivité.
Voici au lien suivant (extrait thèse) un bel exemple de l'utilisation de ce paramètre [datant un peu, texte tapé à la machine (!), le traitement de texte était à peine né].
↑ Haut de page ↑
Le 10.01.2015
Toutes données issues de la base de données du Ministère de l'Ecologie, du Développement Durable et de l'Energie
Deux ouvrages de référence pour appréhender une conception tout à la fois novatrice et s'appuyant sur des expériences originales de l'habitat individuel :
- La Conception Bioclimatique des maisons confortables et économes
S. Courgey & JP Oliva
Terre vivante
- L'isolation thermique écologique, conception, matériaux, mise en oeuvre
JP Oliva & S. Courgey
Terre vivante
- La Conception Bioclimatique des maisons confortables et économes
S. Courgey & JP Oliva
Terre vivante
- L'isolation thermique écologique, conception, matériaux, mise en oeuvre
JP Oliva & S. Courgey
Terre vivante
Information Economie d'Energie : voir Crédit d'impôt (aout 2014) qui est devenu le crédit d'impot pour la transition énergétique, voir ADEME.
↑ Haut de page ↑

Deux notions d'énergie :
- L' énergie primaire est tirée de la nature (soleil, vent, fleuves) ou contenue dans les produits énergétiques tirés de la nature (combustibles fossiles, bois) avant transformation.
- L'énergie secondaire est l'énergie issue de la transformation d'une énergie primaire ou d'une autre énergie secondaire (carburant issu du pétrole brut, électricité produite par une centrale thermique). Branche industrielle appelée branche Energie.(CBE).
- la consommation finale d'énergie (CFE) est égale à la consommation des seuls utilisateurs finals (particuliers, entreprises) autres que celles de la branche énergie.
- la consommation d'énergie primaire (CEP) qui correspond à la consommation totale d'énergie des acteurs économiques.
CEP = CFE + CBE
Depuis la source (énergie primaire) jusqu'à l'énergie utile pour le consommateur, 60% de l'énergie sont perdues dans chaque étape de transformation (faiblesse des rendements cumulés)
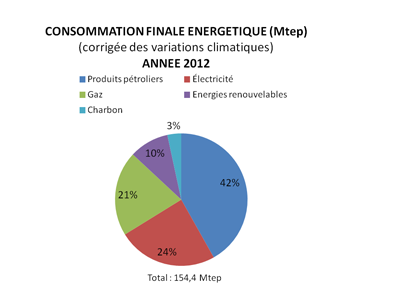
>> 66% de la consommation d'énergie sont issus des combustibles fossiles.
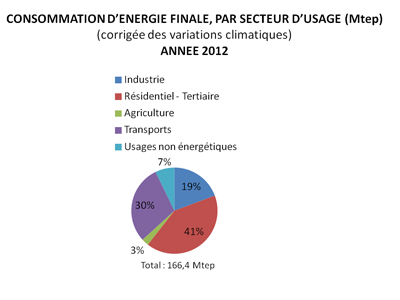
>> Résidentiel/Tertiaire et transports se partagent 71% de la consommation d'énergie.
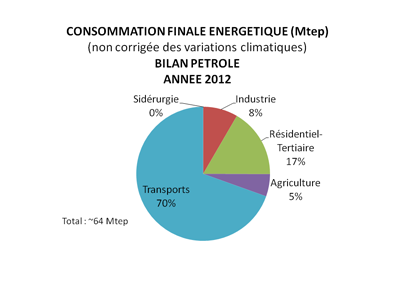
Pour avoir une vision complète et en tirer quelques enseignements il faut ensuite croiser ces données (ex : quelle part de produit pétrolier dans les transports, quelle part de combustibles fossiles dans le résidentiel etc ...?)
>> Ainsi les transports utilisent 71% des produits pétroliers ...
Certes, les 70% des 64Mtep ci-dessus ne couvrent pas tout à fait les 30% des 166,4 Mtep du diagramme précédent : d'autres sources d'énergie (GPL, biocaburants, électricité pour le transport ferroviaire), en faible quantité, sont aussi utilisées.
En seconde position, le Résidentiel/Tertiaire qui "brulent" 17% du pétrole que nous achetons.
Certes, les 70% des 64Mtep ci-dessus ne couvrent pas tout à fait les 30% des 166,4 Mtep du diagramme précédent : d'autres sources d'énergie (GPL, biocaburants, électricité pour le transport ferroviaire), en faible quantité, sont aussi utilisées.
En seconde position, le Résidentiel/Tertiaire qui "brulent" 17% du pétrole que nous achetons.
Ceci simplement pour montrer la complexité du problème.
Quelques petites choses sautent quand même aux yeux :
- les ressources fossiles se feront de plus en plus rares,
conséquence directe, elles seront de plus en plus onéreuses.
- la part des énergies renouvelables est encore très faible .
Quelques petites choses sautent quand même aux yeux :
- les ressources fossiles se feront de plus en plus rares,
conséquence directe, elles seront de plus en plus onéreuses.
- la part des énergies renouvelables est encore très faible .
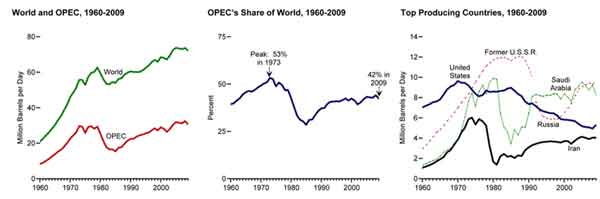
Aujourd'hui 80% des besoins énergétiques mondiaux proviennent des combustibles fossibles (charbon + pétrole + gaz), voir courbe ci-contre.
Deux contraintes incontournables font que ce modèle n'est plus viable à longs termes :
- la raréfaction des ressources.
La production mondiale de pétrole et de gaz atteindra un plateau vers 2040, avant de décliner.
Dans ce scénario, l'hypothèse d'une exploitation de zones à hauts risques écologiques (Arctique, Antarctique) n'est pas retenue (!). ce qui n'est peut-être pas le cas du puissant lobby des industries pétrolières ...
Les réserves estimées en charbon pourraient couvrir des besoins jusqu'au XXII ème siècle. Ce qui n'est pas non plus la solution optimale.
- le réchauffement du climat
Il est avéré que la combustion massive de combustibles fossiles depuis le début du XVIII ième siècle contribue à l'évolution du climat vers un réchauffement via la production de dioxyde de carbone.
Le court terme de cette contrainte climatique est en complet antagonisme avec le § précédent.
Il faut inventer un nouveau mix énergétique faisant appel à des sources d'énergie peu carbonées et à des énergies renouvelables.
Une part de nucléaire, malgré le problème du stockage des déchets et du plutonium, parait difficilement inévitable pour encore quelques décennies.
Il faut y penser de manière urgente.
Et puis souvenons-nous que la principale économie d'énergie est celle que nous n'avons pas consommée ...
Deux contraintes incontournables font que ce modèle n'est plus viable à longs termes :
- la raréfaction des ressources.
La production mondiale de pétrole et de gaz atteindra un plateau vers 2040, avant de décliner.
Dans ce scénario, l'hypothèse d'une exploitation de zones à hauts risques écologiques (Arctique, Antarctique) n'est pas retenue (!). ce qui n'est peut-être pas le cas du puissant lobby des industries pétrolières ...
Les réserves estimées en charbon pourraient couvrir des besoins jusqu'au XXII ème siècle. Ce qui n'est pas non plus la solution optimale.
- le réchauffement du climat
Il est avéré que la combustion massive de combustibles fossiles depuis le début du XVIII ième siècle contribue à l'évolution du climat vers un réchauffement via la production de dioxyde de carbone.
Le court terme de cette contrainte climatique est en complet antagonisme avec le § précédent.
Il faut inventer un nouveau mix énergétique faisant appel à des sources d'énergie peu carbonées et à des énergies renouvelables.
Une part de nucléaire, malgré le problème du stockage des déchets et du plutonium, parait difficilement inévitable pour encore quelques décennies.
Il faut y penser de manière urgente.
Et puis souvenons-nous que la principale économie d'énergie est celle que nous n'avons pas consommée ...
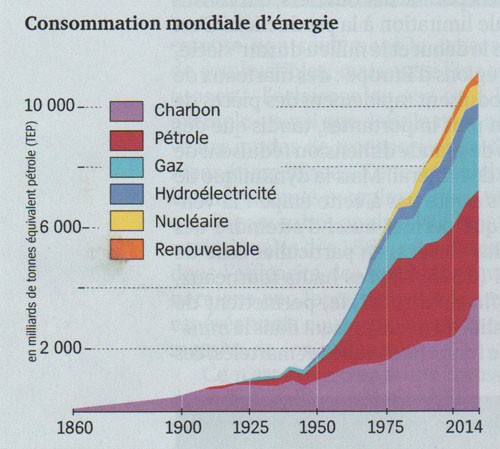
L'Histoire mars 2015
1 Mtep = 1 million de tonnes équivalent pétrole.
Par convention 1 tep = 41,855 GJ = 11,628 MWh = 1 000 m3 de gaz = 7,33 barils de pétrole.
Par convention 1 tep = 41,855 GJ = 11,628 MWh = 1 000 m3 de gaz = 7,33 barils de pétrole.
↑ Haut de page ↑



